ML Wiki
Machine Learning Wiki - A collection of ML concepts, algorithms, and resources.

Eigenvalues and Eigenvectors

linear-algebra

Eigenvalues and Eigenvectors

Eigenvalues and eigenvectors are important in dynamic problems

Introduction

Suppose we have a Matrix $A$. What does it do with a vector?

  • Suppose we multiply $A$ by a vector $\mathbf x$ - and we get a vector $A \mathbf x$
  • what if $A \mathbf x$ is in the same direction as $\mathbf x$?
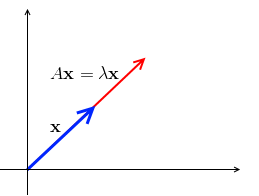
  • Image
  • i.e. if it’s the same direction, then $A \mathbf x = \lambda \mathbf x$ for some $\lambda$
  • such $\mathbf x$ is called ‘‘eigenvector’’ and $\lambda$ is called ‘‘eigenvalue’’

What if $\lambda = 0$?

  • $A \mathbf x = 0 \mathbf x = \mathbf 0$
  • i.e. $\mathbf x \in N(A)$ - the eigenvector $\mathbf x$ belongs to the Nullspace
  • so if $A$ is singular, then $\lambda = 0$ is its eigenvalue

Example: Projection Matrices

Sometimes we can find the eigenvalues by thinking geometrically

  • suppose we have a Projection Matrix $P$
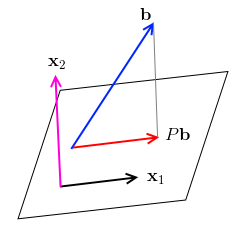
  • Image
  • for a vector $\mathbf b$ that’s not on the place formed by $C(P)$, $\mathbf b$ is not an eigenvector - $P \mathbf b$ is a projection, so they point to different directions
  • suppose there’s a vector $\mathbf x_1$ on the plane. $P \mathbf x_1 = \mathbf x_1$, so all such $\mathbf x_1$ on the plane are eigenvectors with eigenvalues $\lambda = 1$
  • are there other eigenvectors? take any $\mathbf x_2$ orthogonal to the plane: $P \mathbf x_2 = 0 \mathbf x_2 = \mathbf 0$, so $\lambda = 0$
  • so we have two eigenvalues $\lambda = 0$ and $\lambda = 1$

Solving $A \mathbf x = \lambda \mathbf x$

$A \mathbf x = \lambda \mathbf x$

  • let’s rewrite it as $(A - \lambda I) \mathbf x = \mathbf 0$
  • for $\mathbf x \ne \mathbf 0$
  • so the matrix $A - \lambda I$ is singular, thus its Determinant is zero:
  • $\text{det}(A - \lambda I) = 0$ - this is called the ‘‘characteristic equation’’
  • this equation has $n$ roots, so you’ll find $n$ eigenvalues $\lambda_i$
  • then for each $\lambda_i$ we solve the system $A \mathbf x = \lambda_i \mathbf x$ in order to get eigenvectors

$(A - \lambda I) \mathbf x = \mathbf 0$ This eigenvectors are in the Nullspace of $(A - \lambda I)$

Eigenvalues are sometimes called “singular values” because if $\lambda$ is an eigenvalue, then $A - \lambda I$ is singular

Example

Example 1

Let $A = \begin{bmatrix} 3 & 1
1 & 3
\end{bmatrix}$

  • $\text{det}(A - \lambda I) = \begin{bmatrix} 3 - \lambda & 1
    1 & 3- \lambda
    \end{bmatrix} = (3 - \lambda)^2 - 1 = 0$
  • or $(3 - \lambda)^2 = 1$
  • $3 - \lambda = \pm 1$
  • $\lambda_1 = 4, \lambda_2 = 2$

Now can find eigenvectors

  • $(A - \lambda_1 I) \mathbf x_1 = (A - 4 I) \mathbf x_1 = 0$, so $x_1 = \begin{bmatrix} 1 \ 1 \end{bmatrix} \in N(A - 4 I)$
  • $(A - \lambda_2 I) \mathbf x_2 = (A - 2 I) \mathbf x_2 = 0$, so $x_2 = \begin{bmatrix} -1 \ 1 \end{bmatrix} \in N(A - 2 I)$

Example 2: Rotation Matrix

Let $Q = \begin{bmatrix} 0 & -1
1 & 0
\end{bmatrix}$

  • know that $\text{tr } Q = \sum_i \lambda_i$, so $\lambda_1 + \lambda_2 = 0$
  • $\text{det } Q = \lambda_1 \, \lambda_2 = 1$
  • how it’s possible?
  • $\text{det } Q = \begin{vmatrix} -\lambda & -1
    1 & -\lambda
    \end{vmatrix} = \lambda^2 + 1$
  • so $\lambda_1 = i$ and $\lambda_2 = -i$ - complex numbers
  • note that they are complex conjugates
  • this doesn’t happen for Symmetric matrices - they always have real eigenvalues

Properties

Gaussian Elimination changes the eigenvalues of $A$

  • Triangular $U$ has its eigenvalues on the diagonal - but they are not eigenvalues of $A$

eigenvectors can be multiplied by any non-negative constant and will still remain eigenvectors

  • so it’s good to make these vectors unit vectors

Trace and Determinant

$\text{tr } A = \sum\limits_i \lambda_i$

  • $\text{tr } A$ is a Trace of $A$

$\text{det } A = \prod\limits_i \lambda_i$

Eigenvectors and Eigenvalues of $A^k$

if $A \mathbf x = \lambda \mathbf x$ then

  • $A^2 \mathbf x = \lambda A \mathbf x = \lambda^2 \mathbf x$
  • so $\lambda$s are squared when $A$ is squared
  • the eigenvectors stay the same
  • For $A^k$ the eigenvalues are $\lambda_i^k$
  • Eigenvectors stay the same and don’t mix up, only eigenvalues grow

Linear Independence

If all eigenvalues $\lambda_1, \ … \ , \lambda_n$ are different then all eigenvectors $\mathbf x_1, \ … \ , \mathbf x_n$ are linearly independent

  • so any matrix with distinct eigenvalues can be diagonalized

’'’Thm.’’’ $\mathbf x_1, \ … \ , \mathbf x_n$ that correspond to distinct eigenvalues are linearly independent.

Proof

  • Let $\mathbf x_1, \mathbf x_2, \ … \ , \mathbf x_n$ be eigenvectors of some matrix $A$ (so none of them are $\mathbf 0$)
  • and also assume that eigenvalues are distinct, i.e. $\lambda_1 \ne \lambda_2 \ne \ … \ \ne \lambda_n$

$n = 2$ case:

  • consider a linear combination $c_1 \mathbf x_1 + c_2 \mathbf x_2 = \mathbf 0$
  • multiply it by $A$:
    • $c_1 A \, \mathbf x_1 + c_2 A \, \mathbf x_2 = c_1 \lambda_1 \mathbf x_1 + c_2 \lambda_1 \mathbf x_2 = \mathbf 0$
  • then multiply $c_1 \mathbf x_1 + c_2 \mathbf x_2 = \mathbf 0$ by $\lambda_2$:
    • $c_1 \lambda_2 \mathbf x_1 + c_2 \lambda_2 \mathbf x_2 = \mathbf 0$
  • subtract equation 1 from 2 to get the following:
    • $(\lambda_1 - \lambda_2) c_1 \mathbf x_1 = \mathbf 0$
    • since $\lambda_1 \ne \lambda_2$ and $x_1 \ne \mathbf 0$, so it means that $c_1 = 0$
  • by similar argument we see that $c_2 = 0$
  • thus $c_1 \mathbf x_1 + c_2 \mathbf x_2 = \mathbf 0$ because $c_1 = c_2 = 0$
  • or, $\mathbf x_1$ and $\mathbf x_2$ are linearly independent

General case:

  • consider $c_1 \mathbf x_1 + \ … \ + c_n \mathbf x_n = \mathbf 0$
  • multiply by $A$ to get $c_1 \lambda_1 \mathbf x_1 + \ … \ + c_n \lambda_n \mathbf x_n = \mathbf 0$
  • multiply by $\lambda_n$ to get $c_1 \lambda_n \mathbf x_1 + \ … \ + c_n \lambda_n \mathbf x_n = \mathbf 0$
  • subtract them, get $\mathbf x_n$ removed and have the following:
    • $c_1 (\lambda_1 - \lambda_n) \mathbf x_1 + \ … \ + c_{n - 1} (\lambda_{n - 1} - \lambda_n) \mathbf x_{n - 1} = \mathbf 0$
  • do the same again: multiply it with $A$ and with $\lambda_{n-1}$ to get
    • $c_1 (\lambda_1 - \lambda_n) \lambda_1 \mathbf x_1 + \ … \ + c_{n - 1} (\lambda_{n - 1} - \lambda_n) \lambda_{n - 1} \mathbf x_{n - 1} = \mathbf 0$
    • $c_1 (\lambda_1 - \lambda_n) \lambda_{n - 1} \mathbf x_1 + \ … \ + c_{n - 1} (\lambda_{n - 1} - \lambda_n) \lambda_{n - 1} \mathbf x_{n - 1} = \mathbf 0$
    • subtract to get rid of $\mathbf x_{n - 1}$
  • eventually, have this:
  • $(\lambda_1 - \lambda_2) \cdot (\lambda_1 - \lambda_3) \cdot \ … \ \cdot (\lambda_1 - \lambda_{n}) \cdot c_1 \mathbf x_{n} = \mathbf 0$
  • since all $\lambda_i$ are distinct and $x_{n} \ne \mathbf 0$, conclude that $c_1 = 0$
  • can show the same for the rest $c_2, \ … \ , c_n$
  • thus $\mathbf x_1, \mathbf x_2, \ … \ , \mathbf x_n$ are linearly independent

$\square$

Eigenvector Matrix

Suppose we have $n$ linearly independent eigenvectors $\mathbf x_i$ of $A$

  • let’s put them in columns of a matrix $S$ - eigenvector matrix

$S = \Bigg[ \mathop{\mathbb x_1}\limits_| ^| \ \mathop{\mathbb x_2}\limits_|^| \ \cdots \ \mathop{\mathbb x_n}\limits_|^| \Bigg]$ | This matrix is used for Matrix Diagonalization

Usage

Sources

✏️ Edit on GitHub