ML Wiki
Machine Learning Wiki - A collection of ML concepts, algorithms, and resources.

Extensive Form Game

game-theory

Extensive Form Games

Normal Form Games do not reflect time:

  • other players - your opponents - know that you will do, and all actions happen simultaneously

Perfect-Information Game

$A$ - is a (finite) perfect-information game in extensive form

$A$ is defined by $(N, A, H, Z, \chi, \rho, \sigma, u)$

  • $N$ - a set of players
  • $A$ - a set of actions
  • $H$ - a set of non-terminal choice nodes
  • $\chi$ - set of actions available for player in $h \in H$
  • $\rho$ - assigns to each $h \in H$ a player $i \in N$ who chooses an action $a$ in this $h$
  • $Z$ - terminal nodes, where a game ends
  • $\sigma$ - defines a tree (how to get from node h \in H to next note \h_i \in H
  • $u$ - utility function, defined $\forall z \in Z$

The Sharing Game

  • a brother and a sister decide how they want to share 2 dollars
  • Image
  • $p_1$ is the brother, $p_2$ is the sister
  • brother may suggest 2 dollars, 1 dollar and 0 dollars
  • sister accepts or rejects
  • if she accepts, she gets it, the brother gets the rest
  • if she rejects, both get 0

Strategies

  • the brother has 3 strategies
  • the sister 8 - she may choose $2 \times 2 \times 2$ ways to behave

Strategies

A set of strategies consists of the cross product of all possible actions for all nodes

  • these strategies are called the ‘‘pure strategies’’

Example

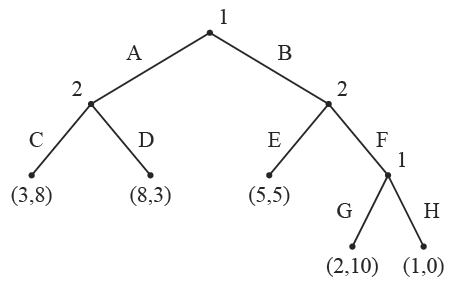  • <img src=”Image” />
  • for player 2 pure strategies are $(C, D) \times (E, F)$
  • for player 1: $(A, B) \times (G, H)$
  • each has 4 strategy

Mixed strategy

  • same as for Normal Form Game
  • but we define the probability distribution over the pure strategies

Nash Equilibrium

  • in this case the best response notion is the same as for Normal Form Games
  • we want to maximize the Expected Utility
  • so the Best Response is a mixed strategy that maximized the utility
  • a strategy profile where each agent best-responds to every other agent is called a Nash Equilibrium

Translation to Normal Form Game

  • Extensive form game can be converted into a Normal Form Game
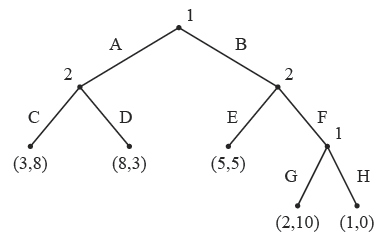  • <img src=”Image” />
  • pure strategies for each agent:
  • <img src=”Image” />
  • the result is called Induced Normal Form Game
    • Although, this form is not compact
    • and we can’t always perform the reverse transformation

Subgame Perfection

  • subgame of $G$ rooted at $H$
    • restriction of $G$ to the descendents of $H$
    • i.e. subtree
  • subgames of $G$
    • all possible subgames of $G$
    • plus $G$ itself
  • subgame perfect equilibrium
    • definition
      • s is a subgame perfect equilibrium
      • if for any subgame $G’$ of $G$
      • the restriction of $s$ to $G’$ is a NE of $G’$
    • rules out all non-credible threats
      • i.e. when player $i$ will never go down that edge
      • but is anyway threatened that if goes, $j$ will pick up bad route
    • example
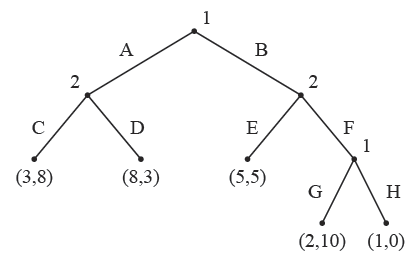      • <img src=”Image” />
      • (A, G), (F, G) is subgame perfect

Backward Induction

  • a way of computing a subgame perfect equilibrium
  • idea: find it in the bottom-most tree, and go up the tree
  • function BackwardIndution
    • if h \in Z
      • return u(z)
    • best_util = -\inf
    • foreach a \in \chi
      • util_at_child = BackwardInduction(\sigma (h, a))
      • if (util_at_child > best_util)
        • best_util = util_at_chile
    • return best_util
  • so it propagates best utility up top

Example: Centipede Game

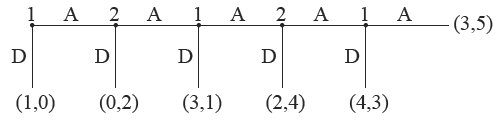  • <img src=”Image” />
  • start from the end:
  • $p_1$ would go $D$ rather then $A$ (4 vs 3)
  • $p_2$ would go $D$ (4 vs 3)
  • $p_1$ would go $D$ (3 vs 2)
  • $p_2$ would go $D$ (2 vs 1)
  • $p_1$ would go $D$ (1 vs 0)
  • so although going would be better, both prefer $D$

Example: Ultimatum Bargaining

  • 10 units to be split between 2 players
  • p1 offers $x \in {0, 1, … 10}$ to pl2
  • p2 accepts or rejects
  • p1 gets 10-x, p2 gets x if pl1 accepts
  • otherwise both get 0
  • tree (pic)
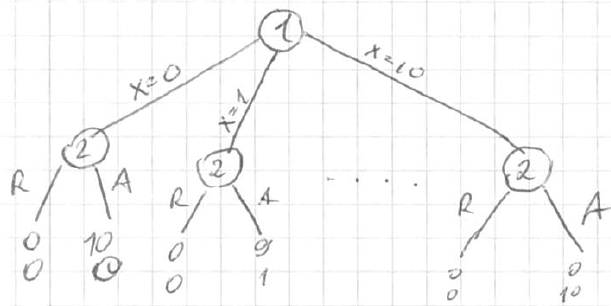    • <img src=”Image” />
    • so, p1 should offer $x > 0$, as p2 will accept any possible amount
    • in fact
      • player may not act this way
      • p2 may expect payoff at least 5
      • subgame perfection doesn’t always match the data

Imperfect-Information

  • poker
    • moves are sequential
    • but there is some uncertainty about moves
    • hidden information   - you sometimes don’t see what others are doing, but it affects your payoff - so we create equivalent classes for some choices
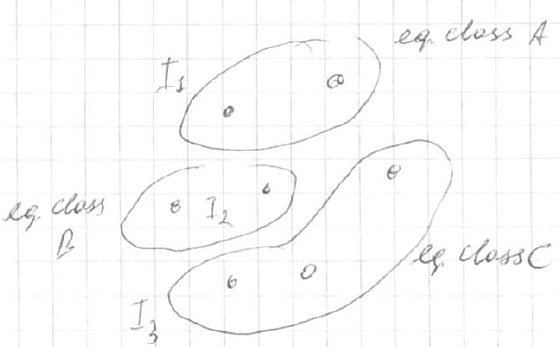    • 2 choices are in $I_1$, two in $I_2$, last three in $I_3$ <img src=”Image” />
    • for items in those classes set of possible actions is the same
    • however payoffs may be different

; definition

  • $A$ is defined by $(N, A, H, Z, \chi, \rho, \sigma, u, I)$

  • where $I = {I_1, … I_n}$ - set of equivalent classes

  • pure strategies
    • product of all possible action of different equality classes
  • example
    • <img src=”Image” />
    • $p_1$ has 4 pure strategies: $Ll, Rr, Lr, Rr$
  • any normal form game can be represented this way
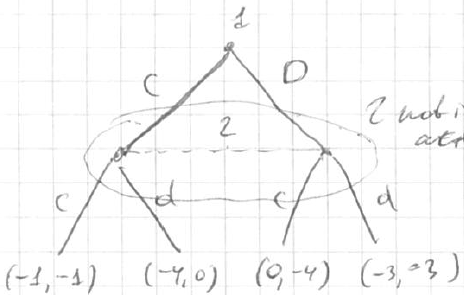    • Prisoners’ Dilemma <img src=”Image” />

Sources

✏️ Edit on GitHub