Fourier Transformation
Goal: to expand a function $f(x)$
- i.e. write it as a linear combination
- $f(x) = a_0 + a_1 \cos x + b_1 \sin x + a_2 \cos 2x + b_2 \sin 2x + \ …$
Basis
These functions $\cos nx$ and $\sin nx$ are orthogonal
- they form an orthogonal basis
- so basis is $\big[ 1, \cos x, \sin x, \cos 2x, \sin 2x, \ … \big]$
- inner product in functions space is $\langle f, g \rangle = \int\limits_0^{2\pi} f(x) g(x) \, dx$
- because these functions are all periodic and analytical, we take the integral only over $[0, 2 \pi]$
- e.g. $\int \sin x \, \cos x \, dx = 0.5 (\sin x)^2 \mathop- so we have orthogonal $\infty$-dimensional basis for this functional space
- and we want to express some function $f(x)$ in this basis
Coefficients
Let’s start with $a_0$
- $f(x) = a_0 1 + a_1 \cos x + b_1 \sin x + a_2 \cos 2x + b_2 \sin 2x + \ …$
- let’s multiply by \cos x and integrate
- $\int f(x) \cos x \, dx = 0 + a_1 \underbrace{\int \cos x \, \cos x \, dx}_{\pi} + 0 + 0 + \ …$
- $\int f(x) \cos x \, dx = a_1 \pi$
- so, $a_1 = \cfrac{1}{\pi} \int f(x) \cos x \, dx$
We can do it for all the coefficients
- this is called “Euler’s formula”
Discrete Fourier Transform
Fourier Matrix
Let $F_n$ be a Fourier matrix:
- $F_n = \begin{bmatrix}
1 & 1 & 1 & \cdots & 1
1 & w^2 & w^2 & \cdots & w^{n - 1}
1 & w^3 & w^4 & \cdots & w^{2(n-1)}
\vdots & \vdots & \vdots & \ddots & \vdots
1 & w^{n-1} & w^{2(n-1)} & \cdots & w^{(n-1)^2}
\end{bmatrix}$ - each element is $(F_n)_{ij} = w^{ij}$ for all $i,j$ (indexes of $F_n$)
- matrix $F_n$ is a symmetric
where $w \in \mathbb C$:
- $w^n = 1$, so $w = \sqrt[n]{1}$
- $w = \exp \left( i \ \cfrac{2\pi}{n} \right) = \cos \cfrac{2\pi}{n} + i \, \sin \cfrac{2\pi}{n}$
- e.g. $w^2 = \exp \left( 2 \ \cfrac{2\pi}{n} \right)$
- $w$ is $n$th root of 1 (“roots of unity”)
Example
- $n = 6, w = \exp \left( 2 \ \cfrac{2\pi}{6} \right) = \exp \left( \cfrac{2\pi}{3} \right)$
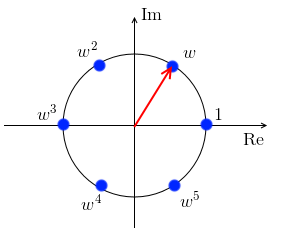
$n = 4$
- $w = \exp \left( i \ \cfrac{2\pi}{4} \right) = i$
- so we have $1, i, i^2 = -1, i^3 = 1$
- thus, $F_4 = \begin{bmatrix}
1 & 1 & 1 & 1
1 & w^2 & w^3 & w^4
1 & w^3 & w^4 & w^5
1 & w^5 & w^5 & w^6
\end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1
1 & i^2 & i^3 & i^4
1 & i^3 & i^4 & i^5
1 & i^5 & i^5 & i^6
\end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1
1 & i & -1 & -i
1 & -1 & 1 & -1
1 & -i & -1 & i
\end{bmatrix}$ - for 4-point Fourier transform: for a vector with 4 components
Columns of $F_n$ are orthogonal
- Let’s check it for $n=4$:
- $\overline{\Big[ 1 \ i \ -1 \ -i \Big]} \begin{bmatrix} 1 \ -i \ -1 \ i \end{bmatrix} = 1 + 1 - 1 - 1 = 0$
- but they are not orthonormal
- e.g. for $F_4$ all columns have length 2
- so let’s define a Fourier Matrix $W_4$ as $W_4 = \cfrac{1}{2} F_4$
- now $W_4^H W_4 = I$
- so let $W_n = \cfrac{1}{\sqrt{n}} F_n$
- we call this $W_n$ a ‘‘Fourier Matrix’’
Discrete Fourier Transform
So, given a matrix $W_n$ and a vector $\mathbf u \in \mathbb C^{n}$ (or in $\mathbb R^{n}$)
- $\mathbf u \cdot W_n$ is the direct transformation
- $\mathbf u \cdot W_n^{-1}$ is the inverse transformation
Fast Fourier Transform
The idea of FFT
- There’s a connection between $W_6$ and $W_3$, $W_8$ and $W_4$, $W_{2n}$ and $W_n$
Example:
- suppose we have $W_{64}$, it’s a $64 \times 64$ matrix
- $w$ is 64th root of 1
- in $W_{32}$, $w$ is 32th root of 1
- so $w_{64}^2 = w_{32}$
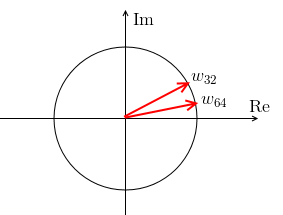
How can we use this fact?
- we want to go from $W_64$ to a matrix $\left[ \begin{array}{c| c} |W_{32} & 0
\hline 0 & W_{32}
\end{array} \right]$ - i.e. factorize $W_{64}$ in terms of $W_{32}$
- can factorize it as $W_{64} = \begin{bmatrix}
I_{32} & D_{32}
I_{32} & -D_{32} \end{bmatrix} \begin{bmatrix} W_{32} & 0
0 & W_{32} \end{bmatrix} P_{64}$- where $P_n$ is a $n \times n$ permutation matrix $P_n = \begin{bmatrix}
1 & & & & \cdots & &
& & 1 & & \cdots & &
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots
& & & & \cdots & 1 &
\hline & 1 & & & \cdots & &
& & & 1 & \cdots & &
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots
& & & & \cdots & & 1
\end{bmatrix}$ - first, in $P$ we have rows with even columns containing $1$, and then, in the second half, rows that contain $1$ in odd columns (here we start indexing columns from 0)
- $P_n$ takes even-numbered components first, and then odd-numbered
- $D_n$ is a diagonal matrix,
- $D_n = \begin{bmatrix}
1 & & & &
& w & & &
& & w^2 & &
& & & \ddots &
& & & & w^{n/2 - 1} \end{bmatrix}$
- where $P_n$ is a $n \times n$ permutation matrix $P_n = \begin{bmatrix}
1 & & & & \cdots & &
- now we can break $W_{32}$ down in the same way| | - $W_{32} = \begin{bmatrix} |I_{16} & D_{16}
I_{16} & -D_{16} \end{bmatrix} \begin{bmatrix} W_{16} & 0
0 & W_{16} \end{bmatrix} P_{32}$ - use recursion
This way we reduce computation from $O(n^2)$ to $\cfrac{n}{2} \, \log_2 n$
Links
- http://www.katjaas.nl/fourier/fourier.html
Sources
- Linear Algebra MIT 18.06 (OCW)
- http://en.wikipedia.org/wiki/DFT_matrix