Lattice

Lattice

a Lattice is a partially ordered set in which every two elements have

• a supremum (also called a least upper bound or join) and
• an infimum (also called a greatest lower bound or meet).

Hasse Diagram

Hasse Diagram [http://en.wikipedia.org/wiki/Hasse_diagram]

• a way of representing finite partially ordered sets

Layer approach

• page 33 - onwards [http://phoenix.inf.upol.cz/~outrata/download/texts/LatDrawing-slides.pdf] - software for drawing

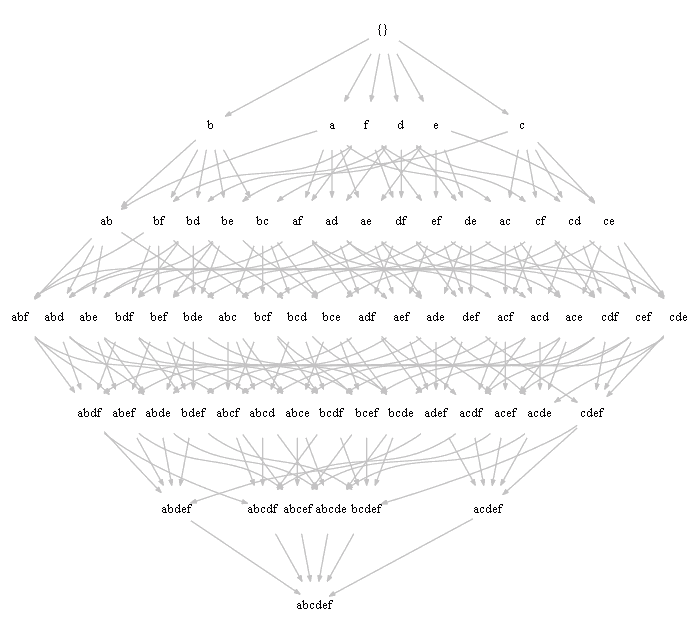
Drawing Powerset with Dot

Generating it in python:

from itertools import chain,combinations,product
from collections import defaultdict

1. from https://docs.python.org/2/library/itertools.html#recipes
def powerset(iterable):
    s = list(iterable)
    return chain.from_iterable(combinations(s, r) for r in range(len(s)+1))

st = 'abcdef'
ps = {''.join(x): set(x) for x in powerset(st)}


dep = defaultdict(list)
for (s1, s2) in product(ps, ps):
    if len(s1) + 1 == len(s2) and ps[s1].issubset(ps[s2]):
        dep[s1].append(s2)

def join_quoted(it): return ','.join(['"%s"' % s for s in it])

for d in sorted(dep, key=len):
    print ' ', '"%s"' % d, '->', join_quoted(dep[d])

Drawing it with dot: ```text only digraph A { node[shape=none, fontsize=10, width=0.3, fixedsize=true] edge[arrowsize=.4,color=grey] nodesep=0.05

”{}” -> “a”,”c”,”b”,”e”,”d”,”f” “c” -> “ac”,”cf”,”ce”,”cd”,”bc” “b” -> “ab”,”bd”,”be”,”bf”,”bc” “a” -> “ac”,”ab”,”ae”,”ad”,”af” “e” -> “ae”,”ef”,”ce”,”be”,”de” “d” -> “ad”,”cd”,”bd”,”df”,”de” “f” -> “af”,”ef”,”cf”,”bf”,”df” “ac” -> “abc”,”acf”,”ace”,”acd” “ab” -> “abc”,”abd”,”abe”,”abf” “ae” -> “abe”,”ade”,”ace”,”aef” “ad” -> “abd”,”adf”,”ade”,”acd” “af” -> “abf”,”adf”,”acf”,”aef” “ef” -> “cef”,”bef”,”aef”,”def” “cf” -> “cef”,”acf”,”cdf”,”bcf” “ce” -> “cde”,”cef”,”ace”,”bce” “cd” -> “cde”,”cdf”,”bcd”,”acd” “bd” -> “bde”,”abd”,”bdf”,”bcd” “bf” -> “abf”,”bdf”,”bcf”,”bef” “de” -> “cde”,”bde”,”ade”,”def” “bc” -> “abc”,”bcd”,”bce”,”bcf” “df” -> “adf”,”bdf”,”cdf”,”def” “be” -> “bde”,”abe”,”bce”,”bef” “cde” -> “acde”,”bcde”,”cdef” “bef” -> “abef”,”bdef”,”bcef” “bde” -> “bdef”,”abde”,”bcde” “abc” -> “abcd”,”abce”,”abcf” “abd” -> “abcd”,”abde”,”abdf” “abe” -> “abef”,”abde”,”abce” “abf” -> “abef”,”abdf”,”abcf” “adf” -> “acdf”,”abdf”,”adef” “ade” -> “acde”,”abde”,”adef” “cef” -> “acef”,”cdef”,”bcef” “bdf” -> “bcdf”,”bdef”,”abdf” “cdf” -> “bcdf”,”acdf”,”cdef” “acf” -> “acdf”,”acef”,”abcf” “ace” -> “acde”,”acef”,”abce” “bcd” -> “bcdf”,”abcd”,”bcde” “bce” -> “bcde”,”bcef”,”abce” “bcf” -> “bcdf”,”bcef”,”abcf” “acd” -> “acde”,”acdf”,”abcd” “aef” -> “abef”,”acef”,”adef” “def” -> “bdef”,”cdef”,”adef” “abef” -> “abdef”,”abcef” “bdef” -> “abdef”,”bcdef” “acde” -> “abcde”,”acdef” “acdf” -> “abcdf”,”acdef” “acef” -> “abcef”,”acdef” “abcd” -> “abcde”,”abcdf” “abde” -> “abcde”,”abdef” “abdf” -> “abdef”,”abcdf” “bcef” -> “abcef”,”bcdef” “bcde” -> “abcde”,”bcdef” “bcdf” -> “bcdef”,”abcdf” “cdef” -> “bcdef”,”acdef” “abce” -> “abcde”,”abcef” “adef” -> “abdef”,”acdef” “abcf” -> “abcef”,”abcdf” “abdef” -> “abcdef” “abcef” -> “abcdef” “bcdef” -> “abcdef” “abcde” -> “abcdef” “abcdf” -> “abcdef” “acdef” -> “abcdef” } ```

Sources

• http://en.wikipedia.org/wiki/Lattice_(order)
• http://en.wikipedia.org/wiki/Hasse_diagram