Mathematical Definition Extraction
Mathematical expressions are hard to understand without the natural language description, so we want to find identifiers in the mathematical expressions and extract their definition from the surrounding text
Example:
- The precision $P$ is defined as $P = \cfrac{w}{w + y}$ where $w$ is the number of correctly labeled pairs and $y$ is the number of incorrectly labeled pairs
- want to extract:
- ($P$, “precision”)
- ($w$, “the number of correctly labeled pairs”)
- ($y$, “the number of incorrectly labeled pairs”)
- Let $e$ be the base of natural logarithm
- ($e$, “the base of natural logarithm”)
Definition
A phrase that defines a mathematical expression consists of three parts: (Kristianto 12)
- definiendum (math expression/identifier - term to be defined) The term—word or phrase—defined in a definition.
- definiens (definition): The word or phrase that defines the definiendum in a definition.
- definitor (relator verb)
We are interested only in parts 1 and 2, and we will call them ‘‘relations’’
An identifier is a mathematical
Automatic Definition Extraction
The definitions of mathematical expressions and identifiers can be found from the natural text description around the expression.
Assumption: the definitions of mathematical expressions are always noun phrases
A noun phrase can be
- just a noun
- compound noun
- compound noun with a clause, prepositional phrase, etc
We have an identifier and want to find what it stands for.
Preprocessing
The typical pipeline is the following:
- Latex documents / Wiki Documents
- => MathML
- => Extract identifiers from MathML
- => Replace formulas with tags
- => Annotate (Math-Aware POS Tagging)
- => Find relations in text
For example:
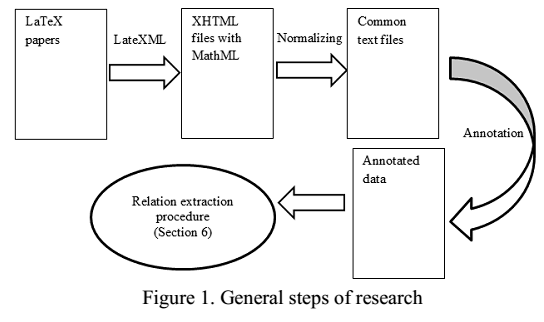
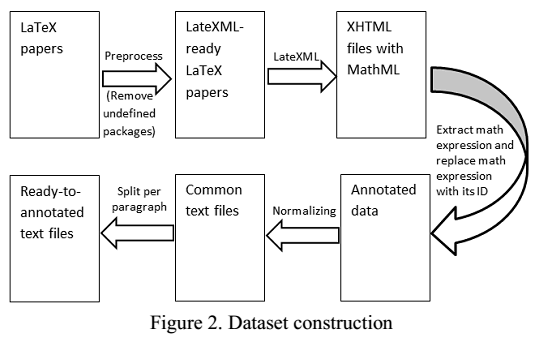
- add MLP flow
Extraction Methods
Nearest Noun Method
Definition is a combination of adjectives and nouns (also sometimes determinants) in the text before the identifier
This way it only can be compound nouns without additional phrases.
E.g:
- “In other words, the bijection $\sigma$ normalizes $G$ in …”
- It will extract relations ($\sigma$, “bijection”)
Papers:
- Grigore, Mihai, Magdalena Wolska, and Michael Kohlhase. “Towards context-based disambiguation of mathematical expressions.” The Joint Conference of ASCM. 2009. (pdf)
- Yokoi, Keisuke, et al. “Contextual analysis of mathematical expressions for advanced mathematical search.” Prof. of 12th International Conference on Intelligent Text Processing and Comptational Linguistics (CICLing 2011), Tokyo, Japan, February. 2011. (pdf)
Pattern Matching Methods
Use patterns to extract definitions
For example,
- DESC IDENTIFIER (this is actually the same as nearest noun method)
-
let set IDENTIFIER denote denotes be DESC - DESC is are denoted defined given as by IDENTIFIER - IDENTIFIER denotes dentore stand stands as by IDENTIFIER - IDENTIFIER is are DESC - DESC is are IDENTIFIER - others
Patterns taken from
- Trzeciak, Jerzy. Writing mathematical papers in English: a practical guide. European Mathematical Society, 1995.
- frequent sentence patterns from Graphs and Combinatorics papers from Springer
Papers:
- Quoc, Minh Nghiem, et al. “Mining coreference relations between formulas and text using Wikipedia.” 23rd International Conference on Computational Linguistics. 2010. (pdf)
- in other papers usually is used as the baseline to compare with
Tools:
- rseq is a convenient tool for Java for doing this
Machine Learning Based Methods
Formulates definition extraction as a binary classification problem
- find candidate pairs (identifier, candidate definition)
- candidates are nouns and noun phrases from the same sentence as the expression
Features:
- sentence patterns (true if one of the patterns can capture this relation - could be separate feature for each pattern)
- if there’s a colon/comma between candidate and identifier
- if there’s another math expression between
- if candidate is inside parentheses and identifier is outside
- word-distance between candidate and identifier
- position of candidate relative to identifier
- text and POS tag of one/two/three preceding and following tokens around the candidate
- unigram/bigram/trigram of previous features
- text of first verb between candidate and identifier
- hop-distance in the dependency tree between the candidate and identifier
- …
Classifiers:
- SVM (linear kernel) (Kristianto14, Yokoi11)
- Conditional Random Fields (Kristianto12)
Papers
- Yokoi, Keisuke, et al. “Contextual analysis of mathematical expressions for advanced mathematical search.” 2011. (pdf)
- Kristianto, Giovanni Yoko, et al. “Extracting definitions of mathematical expressions in scientific papers.” 2012. (pdf)
- Kristianto, Giovanni Yoko, and Akiko Aizawa. “Extracting Textual Descriptions of Mathematical Expressions in Scientific Papers.” D-Lib Magazine 20.11 (2014) (html)
Probabilistic Approaches
Mathematical Language Processing (MLP) Approach:
Rank candidate definitions by probablity and design an information extraction system that shots the most relevant (i.e. probable) definition to the reader to facilitate reading scientific texts with mathematics.
Statistical definition discovery
The idea: the definitions occur very closely to identifiers in sentences.
- extract identifiers from MathML
Two assumptions
- indentifier and its definition occur in the same sentence, so the candidates are taken only from the same sentences (as in the ML approach)
- definitions are likely occur earlier in the document when authors introduce the meaning of an identifier, in subsequent uses the definition is typically not repeated
Ranking:
- each candidate is ranked with the following weighed sum:
- $R(n, \Delta, t, d) = \cfrac{\alpha \, R_{\sigma_d}(\Delta) + \beta \, R_{\sigma_s}(n) + \gamma \, \text{tf}(t, s)}{\alpha + \beta + \gamma}$
- where
- $t$ is the candidate term
- $s$ set of sentences in the document
- $\Delta$ is the distance (the amount of word tokens) between identifier and the candidate term $t$
- $n$ ?
Gaussian:
- $R_{\sigma}(\Delta) = \exp \left( -\cfrac{1}{2} \cdot {\Delta^2 - 1}{\sigma_2} \right)$
- we don’t take the raw distance, but instead use a Gaussian of this distance
- assume that the probability to find a relation at $\Delta = 1$ is maximal
Parameters $\sigma_d$ and $\sigma_s$
- $\sigma_d$ - the standard deviation of Gaussian that models the distance to definition candidate
- manual evaluation showed that $R_{\sigma_d}(1) \approx R_{\sigma_d}(5)$
- i.e. it’s two times more likely to find the real definition at distance $\Delta=1$ than at distance $\Delta=5$
- thus $\sigma_d = \sqrt{\cfrac{12}{\ln 2}}$
- $\sigma_s$
- $\sigma_s = 2 \sqrt{\cfrac{1}{\ln 2}}$
- weights $\alpha, \beta, \gamma$
- $\alpha = \beta = 1$
- $\gamma = 0.1$ because some valid definitions may occur more often than other valid definitions, e.g. “length” vs “Hamiltonian”
Papers:
- Pagael, Schubotz. “Mathematical Language Processing Project.” arXiv preprint arXiv:1407.0167 (2014). (abstract)
Other Ideas
Translation of mathematical formulas to English using machine-translation techniques
- Nghiem, Minh-Quoc, et al. “Towards Mathematical Expression Understanding.” (pdf)
Concept Description Formula:
- relate entire formula to natural language description, e.g.
- $a^2 + b^2 = c^2$ is Pythagorean theorem
Performance Measures
- Precision:
- no of math expresssion with correctly extracted definitions / no of extracted definitions
- recall
- no of math expresssion with correctly extracted definitions / no of expressions with definitions
- F1 = 2PR / (P + R)
Applications
Semantic Search for Mathematical Formulas
Main challenges
- mathematical notation is context-dependent
- same identifier can stand for different mathematical objects
- same mathematical object can be referred to by different identifiers
So same problems as in NLP: a lot of ambiguity and variability
Others
- Mathematical search
- math knowledge bases: Interlinking scientific documents based on content of the formulas
Sources
- Kristianto, Giovanni Yoko, et al. “Extracting definitions of mathematical expressions in scientific papers.” Proc. of the 26th Annual Conference of JSAI. 2012. (pdf)
- Kristianto, Giovanni Yoko, and Akiko Aizawa. “Extracting Textual Descriptions of Mathematical Expressions in Scientific Papers.” D-Lib Magazine 20.11 (2014) (html)
- Pagael, Rober, and Moritz Schubotz. “Mathematical Language Processing Project.” arXiv preprint arXiv:1407.0167 (2014). (abstract)