Allocation Problem
This is a problem of choosing the best position
- to open a new shop
- etc
In Game Theory this problem is known as the ‘‘Median Voter Theorem’’.
The Median Voter Theorem
2 Candidates
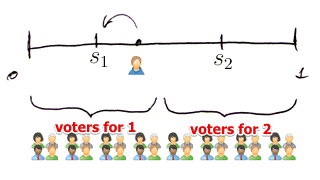
Suppose we have two candidates $s_1$ and $s_2$
- each candidate thinks “what is the best political position to take so the majority vote for me?”
- so suppose the candidates put themselves somewhere between 0 and 1 (extreme left vs extreme right)
- :
- assumptions:
- voters are distributed uniformly
- voters vote for the candidate that is closest to their opinion
Utilities
- with this assumption we use the following utility functions:
- $u_1(s_1, s_2) = \cfrac{s_1 + s_2}{2}$
- $u_2(s_1, s_2) = 1 - u_1(s_1, s_2) = 1 - \cfrac{s_1 + s_2}{2}$ - complimentary part of $u_1$
So there can be the following scenarios
- $s_1 < s_2$
- both take the same position
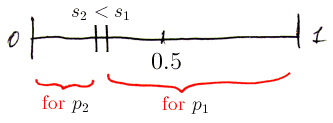
Case 1: $s_1 < s_2$
- not a Nash Equilibrium
- both players want to move: $p_1$ wants to move right and $p_2$ wants to move left
- so there exists another better strategy:
- $u_1(s_1 + \epsilon, s_2) > u_1(s_1, s_2)$
- $p_1$ just moves a little bit to the right and this way gets more votes
Case 2: $s_1 = s_2 < 0.5$
- this is not a Nash Equilibrium either
- since $s_1 = s_2$ they have the same utilities (the voters choose at random from whom to vote)
- $u_1(s_1, s_2) = u_2(s_1, s_2)$
- but this time again there’s an incentive to deviate:
- $u_1(s_1 + \epsilon, s_2) > u_1(s_1, s_2)$
Case 3: $s_1 = s_2 = 0.5$
-
this is a Nash Equilibrium -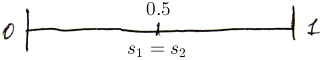 
- no one has an incentive to deviate: - if somebody moves, he gets lower payoff
- $u_1(s_1, s_2) > u_1(s_1 - \epsilon, s_2)$
3 Candidates
But there is no Nash Equilibria for three candidates
Consider this
- there are 3 candidates ${a, b, c}$ who position themselves at the scale [0, 1]
- the positions of the candidates are $s_a, s_b, s_c$
- voters vote to the closest candidate to them
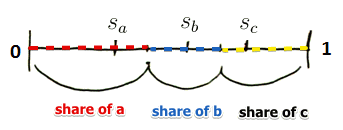
We suppose (without loss of generality) that
- $s_a \leqslant s_b \leqslant s_c$
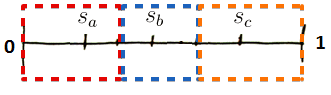
- let $u_a, u_b, u_c$ be the utility functions of $a, b, c$ respectively
Utility functions
| $s_a < s_b < s_c$ ||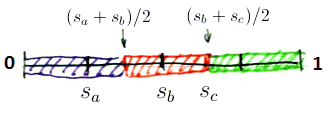 
|| $\left{\begin{matrix} |u^{(1)}_a(s_a, s_b, s_c) = \cfrac{s_a + s_b}{2} \
u^{(1)}_b(s_a, s_b, s_c) = 1 - \cfrac{s_b + s_c}{2}
u^{(1)}_c(s_a, s_b, s_c) = \cfrac{s_b + s_c}{2} - \cfrac{s_a + s_b}{2} \
\end{matrix}\right.$
| $a$ may deviate: $u_a(s_a + \epsilon, s_b, s_c) > u_a(s_a, s_b, s_c)$ || $s_a < s_b = s_c$ ||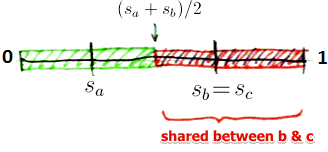 
|| $\left{\begin{matrix} |u^{(2)}_a(s_a, s_b, s_c) = \cfrac{s_a + s_b}{2} \
u^{(2)}_b(s_a, s_b, s_c) = \cfrac{1 - \cfrac{s_a + s_b}{2}}{2}
u^{(2)}_c(s_a, s_b, s_c) = u^{(2)}_b(s_a, s_b, s_c) \
\end{matrix}\right.$
| $a$ may deviate: $u_a(s_a + \epsilon, s_b, s_c) > u_a(s_a, s_b, s_c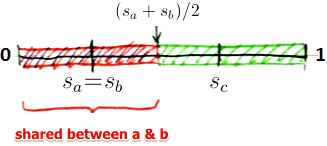)$ || $s_a = s_b < s_c$ || 
|| $\left{\begin{matrix} |u^{(3)}_a(s_a, s_b, s_c) = \cfrac{s_b + s_c}{2 \cdot 2} \
u^{(3)}_b(s_a, s_b, s_c) = u^{(3)}_a(s_a, s_b, s_c)
u^{(3)}_c(s_a, s_b, s_c) = 1 - \cfrac{s_b + s_c}{2} \
\end{matrix}\right.$
| $c$ may deviate: $u_c(s_a, s_b, s_c - \epsilon) > u_c(s_a, s_b, s_c)$ || $s_a = s_b = s_c \ne 0.5$ ||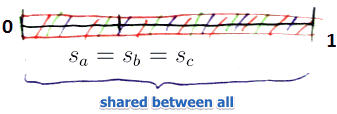 
|| $\left{\begin{matrix} |u^{(4)}_a(s_a, s_b, s_c) = \cfrac{1}{3} \
u^{(4)}_b(s_a, s_b, s_c) = \cfrac{1}{3}
u^{(4)}_c(s_a, s_b, s_c) = \cfrac{1}{3} \
\end{matrix}\right.$
| $a$ may deviate: $u_a(s_a + \epsilon, s_b, s_c) > u_a(s_a, s_b, s_c)$ || $s_a = s_b = s_c = 0.5$ ||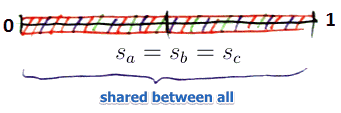 
|| $\left{\begin{matrix} |u^{(4)}_a(s_a, s_b, s_c) = \cfrac{1}{3} \
u^{(4)}_b(s_a, s_b, s_c) = \cfrac{1}{3}
u^{(4)}_c(s_a, s_b, s_c) = \cfrac{1}{3} \
\end{matrix}\right.$
| $a$ may deviate: $u_a(s_a + \epsilon, s_b, s_c) > u_a(s_a, s_b, s_c)$ |
So in all cases there is somebody who wants to deviate:
- No Nash Equilibria
Applications
This is the allocation problem:
- suppose we want to find a location for a new store
- clients that are closer will go to this store
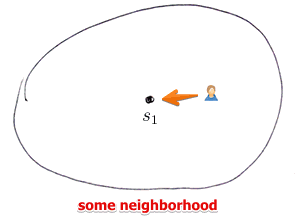
- so they put it in the center
- this is the reason why sometimes big grocery stores are located close to each other