OWL

knowledge-representation semantic-web

OWL

OWL - Web Ontology Language

Several languages

OWL-Full - No limits, but some things can be undecidable
OWL-DL - Descriptive Logic
OWL-Lite - RDFS-Plus, DL-Lite
for logical semantics behind there expressions see Semantic Web Logic

`owl:Restriction`: Restrictions

Allows to describe classes in terms of other things we already modeled

a Restriction in OWL is a Class defined by describing the individuals it contains
owl:Restriction rdfs:subClassOf owl:Class

Kinds of Restrictions

owl:someValuesFrom
- all individuals form which at least one value of the property $P$ comes from some class $C$
- e.g. :AllStarPlayer is a :Player for which at least one value of :playsFor comes from the class :AllStarTeam
- [a owl:Restiction; owl:onProperty :playsFor; owl:someValuesFrom :AllStarTeam]
- if at least one team of this guy is of the class :AllStarTeam $\Rightarrow$ he is an :AllStarPlayer
owl:allValuesFrom
- individuals for which all values of property $P$ come from class $C$
- if there are any members, they all must have the same property
owl:hasValue
- all individuals that have some specific value $a$ for the property $P$
- e.g. :JapanTeams - the set of all baseball :Teams :from :Japan
- e.g. Suppose we have a property :orbitsAround
  - then everything that :orbitsAround :TheSun belongs to the :SolarSystem
  - [a owl:Restriction; owl:onProperty :orbitsAround; owl:hasValue :TheSun]

Best way to use these restrictions:

rdfs:subClassOf
owl:equivalentClass

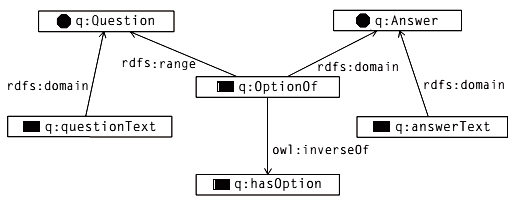
Example: Questionnaire

a questionnaire contains a number of questions
each question has some possible answers
in contrast to a quiz there is no “right” answer
the selection of some answers precludes other questions

Schema (namespace q):

```actionscript 3 q:optionOf a owl:ObjectProperty; rdfs:domain q:Answer; rdfs:range q:Question; owl:inverseOf q:hasOption. q:hasOption a owl:ObjectProperty. q:answerText a owl:DatatypeProperty; rdfs:domain q:Answer; rdfs:range xsd:string. q:questionText a owl:FunctionalProperty, owl:DatatypeProperty; rdfs:domain q:Question; rdfs:range xsd:string. q:Answer a owl:Class. q:Question a owl:Class.

Data (namespace <code>d</code>): 
```actionscript 3
d:WhatProblem a q:Question; 
    q:hasOption d:STV, d:SInternet, d:SBoth; 
    q:questionText "What system are you having trouble with?".
    d:STV a q:Answer; 
    q:answerText "Cable TV". 
d:SInternet a q:Answer; 
    q:answerText "High-speed Internet". 
d:SBoth a q:Answer;
    q:answerText "Both". 
    d:TVsymptom a q:Question; 
    q:questionText "What television symptoms are you having?";
    q:hasOption d:TVSnothing, d:TVSnosound, d:TVStiling, d:TVSreception.
d:TVSnothing a q:Answer; 
    q:answerText "No Picture". 
d:TVSnosound a q:Answer; 
    q:answerText "No Sound". 
d:TVStiling a q:Answer; 
    q:answerText "Tiling". 
    d:TVSreception a q:Answer; 
    q:answerText "Bad reception".

`owl:someValuesFrom`: Answered questions

For each question need to know what’s selected

for that first define a special property q:hasSelectedOption:
- q:hasSelectedOption a owl:ObjectProperty; rdfs:subPropertyOf q:hasOption.
suppose that for d:WhatProblem the selected option is d:STV
- d:WhatProblem q:hasSelectedOption d:STV
a question is answered if it has a selected option (e.g. d:WhatProblem is answered)

q:AnsweredQuestion owl:equivalentClass 
    [a owl:Resrtiction; 
       owl:onProperty q:hasSelectedOption;
       owl:someValuesFrom q:Answer].

`owl:allValuesFrom`: Next Questions

Next questions should depend of what’s been asked and answered

first, define all answers that were selected
q:SelectedAnswer a owl:Class; rdfs:subClassOf q:Answer
to make sure that any option that was selected will appear in this class:
- q:SelectedAnswer rdfs:range q:SelectedAnswer
- e.g. d:WhatProblem q:hasSelectedOption d:STV $\Rightarrow$
- d:STV a q:SelectedAnswer

now define questions that can be asked: q:EnabledQuestion a owl:Class

when some answer is selected, we want to infer that some dependent questions become enabled
each answer potentially makes some other questions enabled
define property q:enablesCandidate for that

```actionscript 3 q:enablesCandidate a owl:ObjectProperty; rdfs:domain q:Asnwer; rdfs:range q:Question.

d:STV q:enablesCandidate d:TVsymptom. d:SBoth q:enablesCandidate d:TVsymptom.

Restriction:
- we want that only answers that were selected enforce this property
- so use <code>owl:allValuesFrom</code> and <code>rdfs:subClassOf</code>

```objective-c
q:SelectedAnswer rdfs:subClassOf [a owl:Restriction; 
    owl:onProperty q:enablesCandidate; 
    owl:allValuesFrom q:EnabledQuestion]

Inference example

assume d:STV is selected: d:STV a q:SelectedAnswer
infer that d:STV a [a owl:Restriction; owl:onProperty q:enablesCandidate; owl:allValuesFrom q:EnabledQuestion]
any individuals related to it by q:enablesCandidate must be members of q:EnabledQuestion
since d:STV q:enablesCandidate d:TVsymptom infer that d:TVsymptom a q:EnabledQuestion

Sets and Counting

Union and Intersection

U a owl:Class; owl:unionOf (ns:A ns:B ...) .
I a owl:Class; owl:intersectionOf (ns:A ns:B ...) .

Example:

suppose we want to know what are enabled high-priority questions

q:CandidateQuestions owl:equivalentClass [
  a owl:Class;
    owl:intersectionOf(q:EnabledQuestion q:HighPriorityQuestion)]

Set Enumeration: Closing the World

Recall the Open World Assumption (see Semantic Web#Main Assumptions)

we can’t be sure that if we don’t have a record about some fact then it doesn’t exist:
it can exist, but maybe we just don’t know about it
sometimes we need to “close the world”: assume we know everything

owl:oneOf

we assume that we can enumerate all the elements of some class
so we put a limit on the AAA slogan: now nobody can say something additional about this topic
so handle it with care
Example: actionscript 3 ss:SolarPlanet rdf:type owl:Class; owl:oneOf (ss:Mercury ss:Venus ss:Earth ss:Mars ss:Jupiter ss:Saturn ss:Uranus ss:Neptune).

Cardinality Restrictions

to express constants on the # of individuals who can participate in some restriction class
for example, a baseball team can have only 9 players

[a owl:Restriction;
   owl:onProperty :hasPlayer;
   owl:cardinality 9]

Also can use:

owl:minCardinality - lower bound
owl:maxCardinality - upper bound

Set Compliment

ex:ClassA owl:complimentOf ex:ClassB

'’compliment’’ - another class whose members are things that don’t belong to this ‘‘complimented’’ class
$A = \Omega - B$

But it includes everything that is not in the complimented class

e.g. bb:MinorLeaguePlayer owl:complimentOf bb:MajorLeaguePlayer
this will include everything else in the universe: players, managers, fans, planets, etc
solution: combine with intersection

bb:MinorLeaguePlayer owl:intersectionOf (
    [a owl:Class; owl:complimentOf bb:MajorLeaguePlayer]
    bb:Player)

so bb:MinorLeaguePlayers are bb:Players who’s not in Major League

Disjoint Sets

:Man owl:disjointSet :Woman

:Irene a :Woman
:Ralph a :Man
infer that :Irene owl:differentFRom :Ralph

Sources

✏️ Edit on GitHub

OWL

OWL

`owl:Restriction`: Restrictions

Kinds of Restrictions

Example: Questionnaire

`owl:someValuesFrom`: Answered questions

`owl:allValuesFrom`: Next Questions

Sets and Counting

Union and Intersection

Set Enumeration: Closing the World

Cardinality Restrictions

Set Compliment

Disjoint Sets

Links

See Also

Sources

OWL

OWL

owl:Restriction: Restrictions

Kinds of Restrictions

Example: Questionnaire

owl:someValuesFrom: Answered questions

owl:allValuesFrom: Next Questions

Sets and Counting

Union and Intersection

Set Enumeration: Closing the World

Cardinality Restrictions

Set Compliment

Disjoint Sets

Links

See Also

Sources

`owl:Restriction`: Restrictions

`owl:someValuesFrom`: Answered questions

`owl:allValuesFrom`: Next Questions