ML Wiki

Petri Nets

Petri nets is a technique for description and analysis of concurrent systems

• very expressive graphical notation
• mathematically formal
• this is an extension of Automata Theory to concurrency
• it's a basis and inspiration of many workflow systems in BPM

Definition

Petri Net

Informally:

• a petri net consists of places (circles) and transitions (squares: activities)
• 
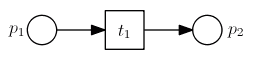
• places can be input/output of transitions
• places represent the states of a system
• transition represent state changes

A petri net is a tuple $(P, T, F)$ where

• $P$ is a finite set of places
• $T$ is a finite set of transitions
• $F \subseteq (P \times T \cup T \times P)$ is a flow relation
  • i.e. this is a set of edges from elements of $P$ to $T$ and from elements of $T$ to $P$
  • 
  • in this case: $F = \{(p_1, t_1), (t_1, p_2)\}$

Every place can contain one or more tokens

• 
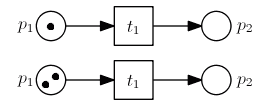
• a token is a piece of work that needs to be processed

Notation:

• $\bullet p$ is a set of all transactions that put tokens to $p$
  • $\bullet p = \{ t \in T \ | \ (t, p) \in F \}$
• $p \bullet$ is a set of all transactions that take tokens from $p$
  • $p \bullet = \{ t \in T \ | \ (p, t) \in F \}$
• $\bullet t$ is a set of all input places of $t$
  • $\bullet t = \{ p \in P \ | \ (t, p) \in F \}$
• $t \bullet$ is a set of all output places of $t$
  • $t \bullet = \{ p \in P \ | \ (p, t) \in F \}$

Example:

• 
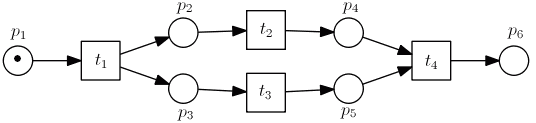
• $\bullet p_3 = \{ t_1 \}$
• $p_3 \bullet = \{ t_3 \}$
• $\bullet t_4 = \{ p_4, p_5 \}$
• $t_4 \bullet = \{ p_6 \}$

Marking

A marking is a state of the net

• shows the distribution of tokens across all places
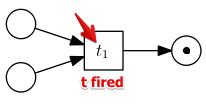
• transition change the state of a bet by firing
• 
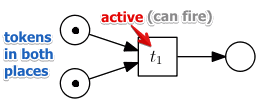
• for a transition $t_1$ in all its input places must be a token
• when $t_1$ fires, it takes exactly one token from each input place and puts exactly one token to each its output place
• 
• 

Formally,

• a marking $M$ of a petri net $N = (P, T, F)$ is a function
• $M: P \mapsto {0, 1, 2, ...}$
• that associates each $p \in P$ with some number: the number of tokens in $p$

Example:

• 
• the marking is $\{(p_1, 1), (p_2, 2), (p_3, 0)\}$

Comparisons

• $M \geqslant M' \iff \forall p \in P: M(p) \geqslant M'(p)$
• $M > M' \iff M \geqslant M' \land M \neq M'$

Enabled Transitions

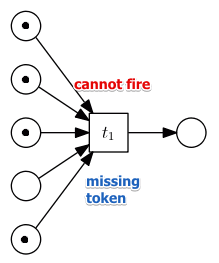
A place is enabled if there is at least one token in all its input places

• transitions change the status of a petri net by firing
• only enabled transitions may fire

def

• a transition is enabled in a marking $M$ $\iff$
• $\forall p \in \bullet t: M(p) > 0$

note that $t$ is active only when there's a token in all input places

• consider this example:
• suppose input tokens correspond to required documents for a visa
• and output token corresponds to an issued visa
• all documents are required: if one is missing - no visa
• 

Example:

• 
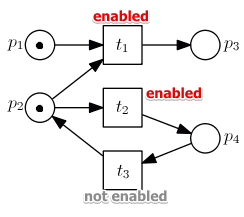
• $t_1$ is enabled: $\bullet t_1 = \{p_1, p_2\}$ and $M(p_1) = M(p_2) = 1$
• $t_2$ is enabled: $\bullet t_2 = \{p_2\}, M(p_2) = 1$
• $t_3$ is not enabled: $\bullet t_3 = \{p_4\}, M(p_4) = 0$

Firing a Transition

A marking $M'$ results from firing an enabled transition $t$ in marking $M$

• $M \to^t M'$ s.t.:
• $\forall p \not \in \bullet t \cup t \bullet: {\color{blue}{M'(p) = M(p)}}$
  • i.e. for all $p$ that are not connected with $t$
• $\forall p \in \bullet t \cap t \bullet: {\color{blue}{M'(p) = M(p)}}$
  • i.e. for all $p$ that are both input and output place for $t$
• $\forall p, p \in \bullet t \land p \not \in t \bullet: {\color{blue}{M'(p) = M(p) - 1}}$
  • $t$ removes a single token from all its input places
• $\forall p, p \not \in \bullet t \land p \in t \bullet: {\color{blue}{M'(p) = M(p) + 1}}$
  • $t$ puts a single token to all its output places

Notation:

• $M \to M' \iff M \to^t M'$ for some transition $t$
  • it reads: $M'$ can be obtained from $M$ by firing some transition (we don't care which one)
• $M \to^* M' \iff M \to^{t_1} M_1 \to^{t_2} M_2 \to^{t_3} ... \to^{t_n} M'$
  • it reads: $M'$ can be obtained from $M$ by firing a sequence of transitions (we don't care which transitions exactly)

Examples

Example 1

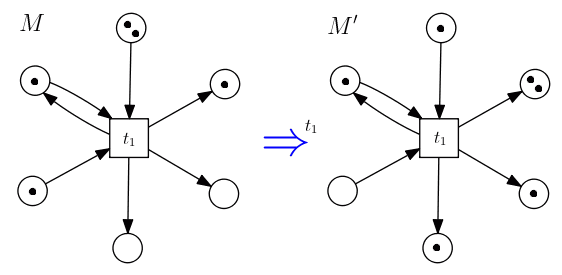
• marking $M$, before firing $t_1$:
  • $t_1$ is enabled
• $t_1$ fires: $M \to^{t_1} M'$
• marking $M'$, after firing $t_1$:
  • $t_1$ is no longer enabled
  • there is no token in one of its input places

Example 2: Candy Storage

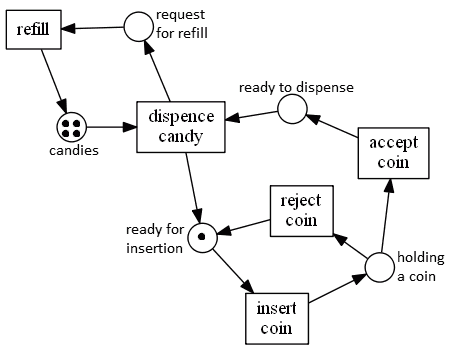
• the candy storage is initially loaded with 4 candies
• when a coin is inserted, it can be either accepted or rejected
• if coin is accepted, a candy is given
• each time a candy is disposed, we request for a new candy
• note that there are manual actions: insert coin, refill; the rest is automatic
  • there's no way to distinguish these actions
  • for example, refill may take a while - it doesn't necessarily have to be immediate

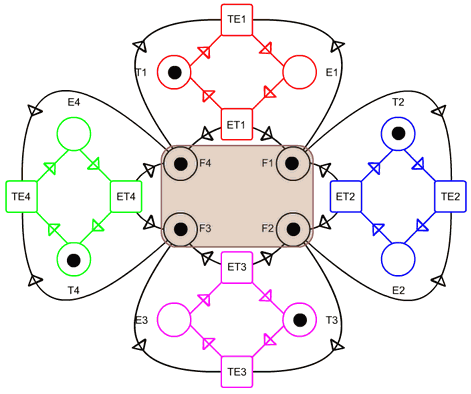
Example 3: Dining Philosophers

It can be seen here:

• http://www.informatik.uni-hamburg.de/TGI/PetriNets/introductions/aalst/philosopher4.swf
• 

Workflow Nets

Main Article: Workflow Nets

Typically a workflow net is a special type of a petri net with

• clear start point
• clear end point
• good for expressing workflows

Soundness

Main Article: Workflow Soundness

Typical Structures

Parallel Execution: And

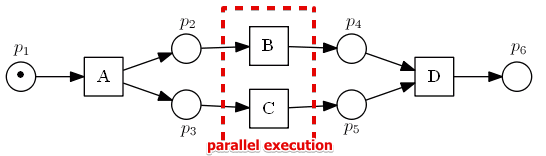
Sequences:

• $A,B,C,D$
• $A,C,B,D$

This construction is called AND and consists of two parts:

• AND-split and
• AND-join

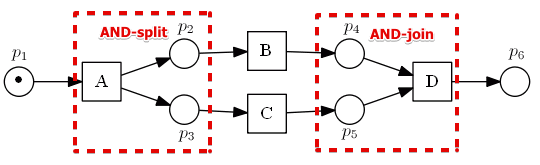
Race Condition: XOR

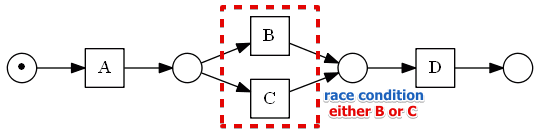
Sequences:

• $A,B,D$
• $A,C,D$
• but not $A,B,C,D$ - can never have it

When there's one input place for two and more transitions, they are in the race condition:

• only one transition can take the token

Alternatively, there could be some other condition

• based on which the transitions decide either to take a token or not

Links

• Examples of petri nets: http://www.informatik.uni-hamburg.de/TGI/PetriNets/introductions/aalst/

Sources

• Business Process Management (ULB)