Q-Q Plot

Q-Q Plot

Probability Plot

A Probability plot is a technique for comparing two data sets

e.g. two empirical observations
or empirical set vs theoretical set

Commonly used:

P-P plot, “Probability-Probability” or “Percent-Percent” plot;
Q-Q plot, “Quantile-Quantile” plot, which is more commonly used.

Normal Probability Plot

It’s a special case of Q-Q plots:

a Q-Q plot against the standard normal distribution;

The normal probability plot is formed by:

Vertical axis: Ordered response values
Horizontal axis: Normal order statistic medians or means (see rankit [https://en.wikipedia.org/wiki/Rankit])

Constructing

order the observations
determine the percentile for each
identify the $z$-score for each percentile
create a Scatterplot
- observation (vertical) vs
- $z$-score (horizontal)

if the data is normally distributed, $z$-scores on the horizontal axis should approximately correspond to their percentiles

R

Example 1

Evaluating the Normal Distribution (see [http://rpubs.com/agrigorev/21480])

load(url("http://www.openintro.org/stat/data/bdims.RData"))
fdims = subset(bdims, bdims$sex == 0)

qqnorm(fdims$hgt, col="orange", pch=19)
qqline(fdims$hgt, lwd=2)

Does it look similar to real Normal Distribution?

it does
let’s simulate the normal distribution and compare

```text only set.seed(123) sim.norm = rnorm(n=length(fdims$hgt), mean=mean(fdims$hgt), sd=sd(fdims$hgt)) qqnorm(sim.norm, col=”orange”, pch=19, main=”Normal Q-Q Plot of simulated data”) qqline(sim.norm, lwd=2)

<img src="http://habrastorage.org/files/471/d9f/11a/471d9f11a690436f96f56ad0c4c544c4.png" alt="Image">


Can try to plot several simulations 

```tera term macro
qqnormsim = function(dat, dim=c(2,2)) {
  par(mfrow=dim)
  qqnorm(dat, main="Normal QQ Plot (Data)")
  qqline(dat)
  for (i in 1:(prod(dim) - 1)) {
    simnorm <- rnorm(n=length(dat), mean=mean(dat), sd=sd(dat))
    qqnorm(simnorm, main = "Normal QQ Plot (Sim)")
    qqline(simnorm)
  }
  par(mfrow=c(1, 1))
}
qqnormsim(fdims$hgt)

Looks like it’s indeed normal

Example 2

(Same data set as in example 1)

Let’s take a look at another dataset

```text only hist(fdims$wgt)

<img src="http://habrastorage.org/files/600/799/aa1/600799aa1fd24b03beed1d063fd7cb0f.png" alt="Image">

Looks a bit skewed 

```text only
qqnorm(fdims$wgt, col="orange", pch=19)
qqline(fdims$wgt, lwd=2)

text only qqnormsim(fdims$wgt)

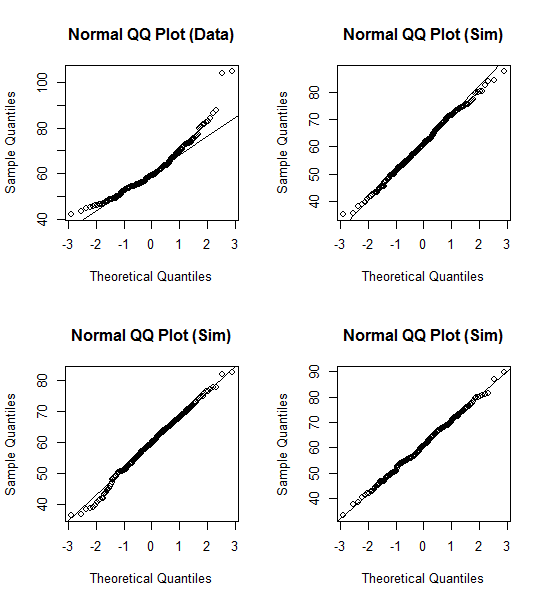
Most likely not normal

Sources

OpenIntro Statistics (book)
https://en.wikipedia.org/wiki/Q-Q_plot
https://en.wikipedia.org/wiki/Normal_probability_plot

✏️ Edit on GitHub