Separability
The monotonicity is a Voting Theory principle that characterizes voting methods for choosing the winner.
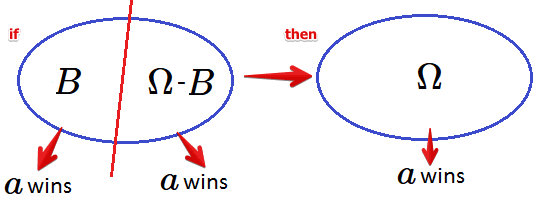
The ‘‘separability’’ principle is satisfied if
- when we split a region $\Omega$ into subregions $B$ and $\Omega - B$ and run the election in both
- if the same candidate $a$ wins in both sub regions $B$ and $\Omega - B$
- then $a$ should win if the election were run for the whole region $\Omega$
Also, when considering the whole rankings:
- suppose for $B$ the ranking is $a_1 > … > a_n$ and for $\Omega - B$ the ranking is $a_1 > … a_n$
- then for $\Omega$ the ranking should also be $a_1 > … > a_n$
It this criterion is not satisfied, then we can split the region into subregions in such a way that we achieve the desired outcome (i.e. it may lead to manipulation)
Methods
Methods that respect Separability:
Methods that don’t respect Separability: