Strongly Connected Components

algorithms graphs

Computing Strong Components

'’strongly connected’’:

you can get to any point to any point within component
example <img src=”” >

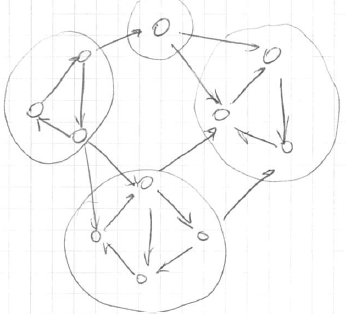idea:

use DFS and mark “leaders”
leaders - points where DFS starts
nodes with the same leader are SCCs

where to start?

it depends on the starting point
with good starting point we may discover a SCC
with bad - the whole graph

Kosaraju’s Two-Pass algorithm

This is a randomized algorithm for finding strongly connected components, consists of 2 DFS passes of the graph.

First pass

compute the “magical” ordering: the finishing times
reverse the graph and run DFS

Example

graph (already reversed) <img src=”” >
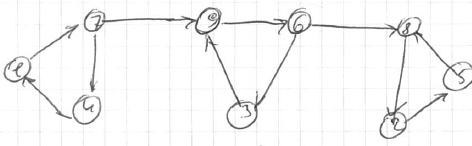t = [7, 3, 1, 8, 2, 5, 9, 4, 6]
order <img src=”” >

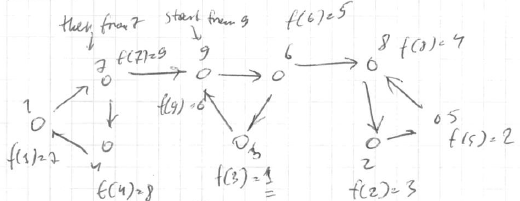Second pass

now we replace ordinal node names with finishing times
and it’s run on the original graph (not the reversed)

Example

second pass <img src=”” >

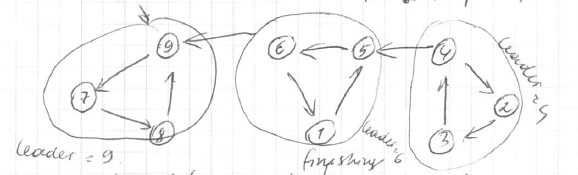Algorithm

It consists of 3 routines: Kosaraju’s, DFS-loop and DFS

Kosaraju’s:

let $G_{\text{rev}}$ be $G$ with all arcs reversed
run DFS-loop on $G_{\text{rev}}$ to compute magic ordering of nodes
let $f(v)$ = “finishing time”
run DFS-loop on $G$ and process nodes in decreasing order of their finishing time

DFS-loop(graph $G$):

global $t$ = 0: number of nodes processed so far
global $s$ = NULL: most recent node from which DFS initiated
for $i$ = $n$ downto $1$
- if $i$ not explored
- $s$ = $i$
- DFS($G$, $i$)

DFS(graph $G$, node $i$):

mark $i$ explored
leader($i$) = node $s$ (where DFS started)
for each $(i, j) \in G$
- if $j$ not explored
- DFS($G$, $j$)
$t$ = $t$ + $1$: finishing time
set $f(i)$ = $t$

Running time: 2DFS = $O(n + m)$

Correctness

idea of the correctness:

maximal finishing time is a sink
if we replace each SCC with just a node
the sink won’t have outgoing edges
first pass finds the sink SCC
second pass “peels off” SCCs one-by-one

Implementation

public class StronglyConnectedComponents {
    private Graph graph;

    private int counter = 0;
    private int currentLeaderVertex = -1;

    private boolean visited[];
    private int leaders[];
    private int finishingTime[];
    private int finishingTimeReversed[];

    public void run() {
        graph = readGraph();
        dfs1Loop();
        dfs2Loop();
    }

    public void dfs1Loop() {
        visited = new boolean[graph.getN()];
        finishingTime = new int[graph.getN()];
        Arrays.fill(finishingTime, -1);
        finishingTimeReversed = new int[graph.getN()];
        Arrays.fill(finishingTimeReversed, -1);

        for (int i = graph.getN() - 1; i >= 0; i--) {
            if (|  visited[i]) { |                currentLeaderVertex = i; |                dfs1(i);
            }
        }
    }

    private void dfs1(int u) {
        visited[u] = true;

        for (int v : graph.reverse(u)) {
            if (|  visited[v]) { |                dfs1(v); |            }
        }

        finishingTime[u] = counter;
        finishingTimeReversed[counter] = u;
        counter++;
    }

    public void dfs2Loop() {
        visited = new boolean[graph.getN()];
        leaders = new int[graph.getN()];
        Arrays.fill(leaders, -1);

        for (int i = graph.getN() - 1; i >= 0; i--) {
            int ft = finishingTimeReversed[i];
            if (|  visited[ft]) { |                currentLeaderVertex = ft; |                dfs2(ft);
            }
        }
    }

    private void dfs2(int u) {
        visited[u] = true;
        leaders[u] = currentLeaderVertex;

        for (int v : graph.adjacent(u)) {
            if (|  visited[v]) { |                dfs2(v); |            }
        }
    }
}

Sources

Algorithms Design and Analysis Part 1 (coursera)

✏️ Edit on GitHub