ML Wiki
Machine Learning Wiki - A collection of ML concepts, algorithms, and resources.

Topological Ordering

algorithms graphs sorting

Topological Ordering

A ‘‘topological ordering’’ for a directed graph $G$ is a labelling $f$ of $G$’s nodes such that

  • the $f(v)$’s are the set ${1, 2, …, n}$
  • $(u, v) \in G$ => $f(u) < f(v)$
  • all edges go forward

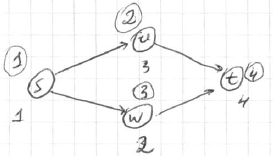
Example:

  • graph <img src=”Image” >
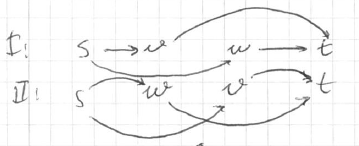  • possible orderings <img src=”Image” >

Motivation:

  • sequence tasks while respecting all constains
    • courses at uni with prerequisites

Straightforward solution

  • every directed graph has a ‘‘sink’’ vertex <img src=”Image” >
  • compute backwards, finding a sink on each iteration

Idea:

  • let $v$ be sink of $G$
  • set $f(v) = n$
  • recurse on $G - {v}$

But it can be computed using Depth-First Search very quickly

DFS solution

  • dfs finds a sink
  • and unfolds backwards numerating the vertices

Consists of 2 routines: DFS-loop and DFS

DFS-loop(graph $G$):

  • mark all vertices not explored
  • current label = $n$
  • for each vertex $v$
    • if $v$ not explored
    • DFS($G$, $v$)

DFS(graph $G$, vertex $s$):

  • for every edge $(s, v)$
    • if $v$ not explored
    • mark $v$ explored
    • DFS($G$, $v$)
  • set $f(s)$ = current label
  • current label = current label - 1

Cycles

if $G$ has a [directed] cycle, it has no topological ordering. It is possible to modify the algorithm so it will inform about cycles.

Idea: instead of marking the vertices as explored, mark them with two colors:

  • one color means “the vertex is being processed”
  • another color means “the vertex has been processed”

Modifications:

  • check if vertex $s$ is already ‘‘being proceed’’ - and if so, report a cycle
  • mark the vertex as ‘‘being processed’’
  • proceed as usually
  • before leaving the routine, mark the vertex as ‘‘done’’

Implementation

public class TopologicalOrdering {
    private final List<String> vertices;
    private final Graph graph;
    private final Map<String, Status> visitedVertices;
    private final List<String> result = Lists.newLinkedList();

    // some initialization

    private static enum Status {
        STARTED, DONE;
    }

    public List<Rule> run() {
        for (String vertex : vertices) {
            if (|  visitedVertices.containsKey(vertex)) { |                dfs(graph, vertex); |            }
        }

        return result;
    }

    private void dfs(Graph graph, String vertex) {
        Status status = visitedVertices.get(vertex);
        if (status == Status.STARTED) {
            throw new IllegalStateException("Look ma I got a cycle|  "); |        } |
        if (status == Status.DONE) {
            return;
        }

        visitedVertices.put(vertex, Status.STARTED);

        for (String to : graph.adjacent(vertex)) {
            dfs(graph, to);
        }

        visitedVertices.put(vertex, Status.DONE);
        result.add(vertex);
    }
}

See also

Sources

✏️ Edit on GitHub