Voting Theory Examples
Different examples from Voting Theory that illustrate some interesting properties.
Example 1
This is an example in which different voting mechanisms of Voting Theory produce different results.
Consider this example:
- $N = 24$
- $A = { t, x, y, z }$
Votes:
- 5 votes $x > y > z > t$
- 4 votes $x > z > y > t$
- 2 votes $t > y > x > z$
- 6 votes $t > y > z > x$
- 8 votes $z > y > x > t$
- 2 votes $t > z > y > x$
Example 1: Plurality Voting
- The global ranking is
- $t > x > z > y $
- $(10 > 9 > 8 > 0)$
Therefore $t$ gets elected
-
But 17 voters (the majority ) prefer $x$ to $t$ - Condorcet Fairness criterion is not satisfied
Example 1: Two-Round Voting
Round 1:
- $x$ and $t$ are selected
Round 2:
- remove all other candidates:
- 5 + 4 + 8 = 17 votes $x > t$
- 2 + 6 + 2 = 10 votes $t > x$
$x$ wins
-
but $y$ is preferred to $x$ by 18 voters (the majority ) - Condorcet Fairness criterion is not satisfied
Example 1: Borda’s Rule
The Borda Scores:
- $B(t) = 57$
- $B(x) = 5 \cdot 4 + 4 \cdot 4 + 2 \cdot 2 + 6 \cdot 1 + 8 \cdot 2 + 2 \cdot 1 = 64$
- $B(y) = 75$
- $B(z) = 74$
$y$ wins
- note that $t$ is the last one, but for the Plurality Voting he is the winner
Example 1: Condorcet’s Rule
Pairwise comparison:
- $t,x: n_{xt} = 17, n_{tx} = 10 \Rightarrow x > t$
- $x,y: n_{xy} = 9, n_{yx} = 18 \Rightarrow y > x$
- $t,y: n_{ty} = 10, n_{yt} = 17 \Rightarrow y > t$
- $x,z: n_{xz} = 11, n_{zx} = 16 \Rightarrow z > x$
- $y,z: n_{yz} = 13, n_{zy} = 14 \Rightarrow z > y$
- $t,z: n_{tz} = 10, n_{zt} = 17 \Rightarrow z > t$
- We build the preference graph for this:
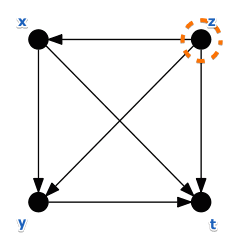
We see that $z$ is the winner