ML Wiki

Voting Theory Exercises

Define $a \ B \ b$ as

$a \ B \ b \iff n_{ab} \geqslant 6$ where $n_{ab}$ is the number of people who rank $a$ before $b$ (like in Condorcet's Rule)

This voting system is very similar to the Condorcet's Rule

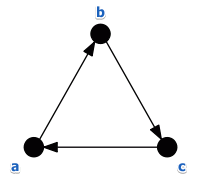
We can show that it means to be transitive:

ex-transitivity.png
i.e. if there exists a loop then there can be no transitivity
so it suffices to show that there can be cycles and it will answer both questions

Consider the following ranking:

Now calculate the $B$ relationship:

We have a cycle:

Define $a \ B \ b$ as

$a \ B \ b \iff n_{ab} \geqslant 7$ where $n_{ab}$ is the number of people who rank $a$ before $b$

In this case $B$ also is not always transitive.

Consider the following example:

$4: a > b > c$
$3: b > c > a$
$3: c > a > b$
in this case there are not enough votes to have an edge $c \to a$
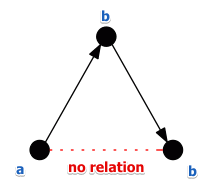
note that his shows that the relation $B$ is not complete (this can also be the case for the previous exercise)

And there can be no cycles: too few voters for this

consider the case with 3 candidates: $A = \{a, b, c\}$
there are 6 possible individual rankings for elements from $A$: there are 3! permutations of $A$
- $R_1: a < b < c$ -- $n_1$ voters
- $R_2: a < c < b$ -- $n_2$ voters
- $R_3: b < a < b$ -- $n_3$ voters
- $R_4: b < c < a$ -- $n_4$ voters
- $R_5: c < a < b$ -- $n_5$ voters
- $R_6: c < b < a$ -- $n_6$ voters
- $n_i$ - the number of voters with ranking $R_i$
to have a cycle we need to have:
- $n_{ab} = n_1 + n_2 + n_6 \geqslant 7$
- $n_{ba} = n_1 + n_3 + n_4 \geqslant 7$
- $n_{ca} = n_4 + n_5 + n_6 \geqslant 7$
let's sum up these
- $2 \cdot n_1 + n_2 + n_3 + 2 \cdot n_4 + n_5 + 2 \cdot n_6 \geqslant 21$ (1)
recall that we have only 10 voters:
- $n_1 + n_2 + n_3 + n_4 + n_5 + n_6 = 10$ (2)
now let's calculate (1) - (2):
- $n_1 + n_4 + n_6 \geqslant 11$
- this cannot happen: we have only 10 voters
contradiction