ML Wiki

Eigenvalues and Eigenvectors

Eigenvalues and Eigenvectors

Eigenvalues and eigenvectors are important in dynamic problems


Suppose we have a Matrix $A$. What does it do with a vector?

  • Suppose we multiply $A$ by a vector $\mathbf x$ - and we get a vector $A \mathbf x$
  • what if $A \mathbf x$ is in the same direction as $\mathbf x$?
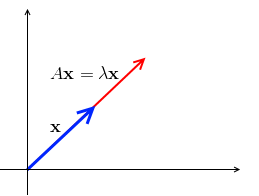
  • a57974fa1416425bb4f296df8ea6b507.png
  • i.e. if it's the same direction, then $A \mathbf x = \lambda \mathbf x$ for some $\lambda$
  • such $\mathbf x$ is called eigenvector and $\lambda$ is called eigenvalue


What if $\lambda = 0$?

  • $A \mathbf x = 0 \mathbf x = \mathbf 0$
  • i.e. $\mathbf x \in N(A)$ - the eigenvector $\mathbf x$ belongs to the Nullspace
  • so if $A$ is singular, then $\lambda = 0$ is its eigenvalue


Example: Projection Matrices

Sometimes we can find the eigenvalues by thinking geometrically

  • suppose we have a Projection Matrix $P$
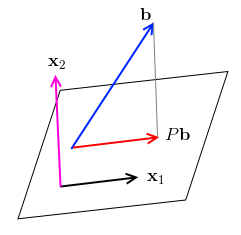
  • 7d3f88ed987c48e7bebacc5a3f336e21.png
  • for a vector $\mathbf b$ that's not on the place formed by $C(P)$, $\mathbf b$ is not an eigenvector - $P \mathbf b$ is a projection, so they point to different directions
  • suppose there's a vector $\mathbf x_1$ on the plane. $P \mathbf x_1 = \mathbf x_1$, so all such $\mathbf x_1$ on the plane are eigenvectors with eigenvalues $\lambda = 1$
  • are there other eigenvectors? take any $\mathbf x_2$ orthogonal to the plane: $P \mathbf x_2 = 0 \mathbf x_2 = \mathbf 0$, so $\lambda = 0$
  • so we have two eigenvalues $\lambda = 0$ and $\lambda = 1$


Solving $A \mathbf x = \lambda \mathbf x$

$A \mathbf x = \lambda \mathbf x$

  • let's rewrite it as $A \mathbf x - \lambda \mathbf x = (A - \lambda I) \mathbf x = \mathbf 0$
  • so, $(A - \lambda I) \mathbf x = \mathbf 0$ for $\mathbf x \ne \mathbf 0$
  • we want the vector to be non-zero, and it's only possible when the matrix $A - \lambda I$ is singular: that is, the columns of this matrix should be linearly dependent, so it's possible to get the zero verctor
  • the matrix $A - \lambda I$ is singular when its Determinant is zero
  • this, we need to solve $\text{det}(A - \lambda I) = 0$ - this is called the characteristic equation of $A$
  • this equation is an $n$th order polynomial and has $n$ roots, so you'll find $n$ eigenvalues $\lambda_i$
  • Eigenvalues are sometimes called "singular values" because if $\lambda$ is an eigenvalue, then $A - \lambda I$ is singular


Finding the eigenvector

  • Look at the $(A - \lambda I) \mathbf x = \mathbf 0$
  • The corresponding eigenvector $\mathbf x$ is in the Nullspace of $A - \lambda I$
  • So we need to solve this equation to get the vector
  • Since the matrix is singular, there are multiple such eigenvectors - same direction, but different scale
  • We just fix some scale and find the direction


Examples

Example 1

Let [math]A = \begin{bmatrix} 3 & 1 \\ 1 & 3 \\ \end{bmatrix}[/math]

  • [math]\text{det}(A - \lambda I) = \begin{bmatrix} 3 - \lambda & 1 \\ 1 & 3- \lambda \\ \end{bmatrix} = (3 - \lambda)^2 - 1 = 0[/math]
  • or $(3 - \lambda)^2 = 1$
  • $3 - \lambda = \pm 1$
  • $\lambda_1 = 4, \lambda_2 = 2$

Now can find eigenvectors

  • $(A - \lambda_1 I) \mathbf x_1 = (A - 4 I) \mathbf x_1 = 0$, so $x_1 = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \in N(A - 4 I)$
  • $(A - \lambda_2 I) \mathbf x_2 = (A - 2 I) \mathbf x_2 = 0$, so $x_2 = \begin{bmatrix} -1 \\ 1 \end{bmatrix} \in N(A - 2 I)$


Example 2

Let [math]A = \begin{bmatrix} 0 & 1 \\ -2 & 3 \\ \end{bmatrix}[/math]

  • need to solve $\text{det } A = 0$:
  • $- \lambda (3 - \lambda) + 2 = 0$
  • $\lambda_{1,2} = \cfrac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \cfrac{3 \pm \sqrt{9 - 4 \cdot 2}}{2} = \cfrac{3 \pm 1}{2}$
  • so $\lambda_1 = 1$ and $\lambda_2 = 2$

Eigenvector $A \mathbf v_1 = \lambda_1 \mathbf v_1$

  • $(A - \lambda_1 I) \mathbf v_1 = \mathbf 0$
  • [math]\begin{bmatrix} 0 - 1 & 1 \\ -2 & 3 - 1 \\ \end{bmatrix} = \begin{bmatrix} -1 & 1 \\ -2 & 2 \\ \end{bmatrix}[/math], [math]\begin{bmatrix} -1 & 1 \\ -2 & 2 \\ \end{bmatrix} \mathbf v_1 = \mathbf 0[/math]
  • Reduce the matrix to upper triangular form - and then we see that there's zeros on the last row (the matrix is singular)
    • [math]\begin{bmatrix} -1 & 1 \\ 0 & 0 \\ \end{bmatrix}[/math]
    • can fix some value of $v_{12}$, e.g. $v_{12} = 1$
    • then $v_{11} = 1$
  • so [math]\mathbf v_1 = c \cdot \begin{bmatrix} 1 \\ 1 \\ \end{bmatrix}[/math] where $c$ is some constant


Example 3: Rotation Matrix

Let [math]Q = \begin{bmatrix} 0 & -1 \\ 1 & 0 \\ \end{bmatrix}[/math]

  • know that $\text{tr } Q = \sum_i \lambda_i$, so $\lambda_1 + \lambda_2 = 0$
  • [math]\text{det } Q = \lambda_1 \, \lambda_2 = 1[/math]
  • how it's possible?
  • [math]\text{det } Q = \begin{vmatrix} -\lambda & -1 \\ 1 & -\lambda \\ \end{vmatrix} = \lambda^2 + 1[/math]
  • so $\lambda_1 = i$ and $\lambda_2 = -i$ - complex numbers
  • note that they are complex conjugates
  • this doesn't happen for Symmetric matrices - they always have real eigenvalues


Properties

  • Gaussian Elimination changes the eigenvalues of $A$
    • Triangular $U$ has its eigenvalues on the diagonal - but they are not eigenvalues of $A$
  • eigenvectors can be multiplied by any non-negative constant and will still remain eigenvectors
    • so it's good to make these vectors unit vectors


Trace and Determinant

  • $\text{tr } A = \sum\limits_i \lambda_i$
    • $\text{tr } A$ is a Trace of $A$
  • $\text{det } A = \prod\limits_i \lambda_i$

TODO: prove it


Eigenvectors and Eigenvalues of $A^k$

if $A \mathbf x = \lambda \mathbf x$ then

  • $A^2 \mathbf x = \lambda A \mathbf x = \lambda^2 \mathbf x$
  • so $\lambda$s are squared when $A$ is squared
  • the eigenvectors stay the same
  • For $A^k$ the eigenvalues are $\lambda_i^k$
  • Eigenvectors stay the same and don't mix up, only eigenvalues grow
  • this is used in Power Iteration and other methods for finding approximate values of eigenvalues and eigenvectors


Linear Independence

If all eigenvalues $\lambda_1, \ ... \ , \lambda_n$ are different then all eigenvectors $\mathbf x_1, \ ... \ , \mathbf x_n$ are linearly independent

  • so any matrix with distinct eigenvalues can be diagonalized


Thm. $\mathbf x_1, \ ... \ , \mathbf x_n$ that correspond to distinct eigenvalues are linearly independent.


Proof

  • Let $\mathbf x_1, \mathbf x_2, \ ... \ , \mathbf x_n$ be eigenvectors of some matrix $A$ (so none of them are $\mathbf 0$)
  • and also assume that eigenvalues are distinct, i.e. $\lambda_1 \ne \lambda_2 \ne \ ... \ \ne \lambda_n$


$n = 2$ case:

  • consider a linear combination $c_1 \mathbf x_1 + c_2 \mathbf x_2 = \mathbf 0$
  • multiply it by $A$:
    • $c_1 A \, \mathbf x_1 + c_2 A \, \mathbf x_2 = c_1 \lambda_1 \mathbf x_1 + c_2 \lambda_1 \mathbf x_2 = \mathbf 0$
  • then multiply $c_1 \mathbf x_1 + c_2 \mathbf x_2 = \mathbf 0$ by $\lambda_2$:
    • $c_1 \lambda_2 \mathbf x_1 + c_2 \lambda_2 \mathbf x_2 = \mathbf 0$
  • subtract equation 1 from 2 to get the following:
    • $(\lambda_1 - \lambda_2) c_1 \mathbf x_1 = \mathbf 0$
    • since $\lambda_1 \ne \lambda_2$ and $x_1 \ne \mathbf 0$, so it means that $c_1 = 0$
  • by similar argument we see that $c_2 = 0$
  • thus $c_1 \mathbf x_1 + c_2 \mathbf x_2 = \mathbf 0$ because $c_1 = c_2 = 0$
  • or, $\mathbf x_1$ and $\mathbf x_2$ are linearly independent


General case:

  • consider $c_1 \mathbf x_1 + \ ... \ + c_n \mathbf x_n = \mathbf 0$
  • multiply by $A$ to get $c_1 \lambda_1 \mathbf x_1 + \ ... \ + c_n \lambda_n \mathbf x_n = \mathbf 0$
  • multiply by $\lambda_n$ to get $c_1 \lambda_n \mathbf x_1 + \ ... \ + c_n \lambda_n \mathbf x_n = \mathbf 0$
  • subtract them, get $\mathbf x_n$ removed and have the following:
    • $c_1 (\lambda_1 - \lambda_n) \mathbf x_1 + \ ... \ + c_{n - 1} (\lambda_{n - 1} - \lambda_n) \mathbf x_{n - 1} = \mathbf 0$
  • do the same again: multiply it with $A$ and with $\lambda_{n-1}$ to get
    • $c_1 (\lambda_1 - \lambda_n) \lambda_1 \mathbf x_1 + \ ... \ + c_{n - 1} (\lambda_{n - 1} - \lambda_n) \lambda_{n - 1} \mathbf x_{n - 1} = \mathbf 0$
    • $c_1 (\lambda_1 - \lambda_n) \lambda_{n - 1} \mathbf x_1 + \ ... \ + c_{n - 1} (\lambda_{n - 1} - \lambda_n) \lambda_{n - 1} \mathbf x_{n - 1} = \mathbf 0$
    • subtract to get rid of $\mathbf x_{n - 1}$
  • eventually, have this:
  • $(\lambda_1 - \lambda_2) \cdot (\lambda_1 - \lambda_3) \cdot \ ... \ \cdot (\lambda_1 - \lambda_{n}) \cdot c_1 \mathbf x_{n} = \mathbf 0$
  • since all $\lambda_i$ are distinct and $x_{n} \ne \mathbf 0$, conclude that $c_1 = 0$
  • can show the same for the rest $c_2, \ ... \ , c_n$
  • thus $\mathbf x_1, \mathbf x_2, \ ... \ , \mathbf x_n$ are linearly independent


$\square$

Eigenvector Matrix

Suppose we have $n$ linearly independent eigenvectors $\mathbf x_i$ of $A$

  • let's put them in columns of a matrix $S$ - eigenvector matrix

$S = \Bigg[ \mathop{\mathbb x_1}\limits_|^| \ \mathop{\mathbb x_2}\limits_|^| \ \cdots \ \mathop{\mathbb x_n}\limits_|^| \Bigg]$

This matrix is used for Matrix Diagonalization


Usage


Sources

Retrieved from "http://mlwiki.org/index.php?title=Eigenvalues_and_Eigenvectors&oldid=783"