ML Wiki

ELECTRE

This is a method from the family of outranking (i.e. based on pair-wise comparison) MCDA methods. The result is a partial ordering of alternatives (see Partial Order Preference Structure)

Here:

• ELECTRE I

ELECTRE I chooses alternatives that are preferred by the majority of the criteria and which don’;t cause an unacceptable level of discontentment on other criteria.

Preferences

Main idea

When we say $a \ P \ b$?

• (1) if we have a lot of criteria for which $u_i(a) > u_i(b)$ (where $u_i$ - some utility function)
• (2) and we have no strong arguments that say the opposite of (1)

The ELECTRE methods are based on two concepts:

• Concordance Index
• Discordance Index

Concordance Index

Or quantification of positive arguments

For ELECTRE 1, when comparing $a$ and $b$

• identify all criteria $g_j$ such that $g_j(a) \geqslant g_j(b)$
• for all such criteria $g_j$ sum their weights $w_j$,
• let $W$ be the sum of all weights: $W = \sum_i w_i$ (we use this for normalization)
• define the concordance index as:

  $c(a, b) = \cfrac{1}{W} \sum_{j: g_j(a) \geqslant g_j(b)} w_j$

Note that weight should sum up to 1

There are two extreme cases:

• $c(a, b) = 1$: all criteria for $a$ are better than for $b$ (Unanimity)
  • have very good reasons to say $a \ P \ b$
• $c(a, b) = 0$: there is no criteria in which $a$ better than $b$

Discordance Index

Or quantification of negative arguments

We want to find a strong argument against $a \ P \ b$

• if we find such an argument then we cannot say that $a \ P \ b$

For ELECTRE I, define $d(a, b)$ as

• 0 when $\forall j: g_j(a) \geqslant g_j(v)$ (none when there's Unanimity)
• if $\exists g_i: g_i(b) \geqslant g_i(a)$ then we have an argument against $a \ P \ b$
• in this case we want to identify the largest difference between $a$ and $b$:
  • $\cfrac{1}{\delta} \max_j [g_j(b) - g_j(a)]$
  • $\delta$ is normalization factor: $\delta = \max_{i,c,d} [g_i(c) - g_i(d)]$

Another way

• let $D$ be the set of cases where we list cases that cannot be compared
• if for a pair of alternatives $(a, b)$ there exists a criteria $g_i$ s.t. $(g_i(a), g_i(b)) \in D$ then we cannot compare these alternatives

Outranking Preference Relation

For ELECTRE I we define $S \equiv P \lor I$ as: (the "as good as relations", also see Voting Theory Relations)

• $a \ S \ b \iff$
  • (1) $c(a, b) \geqslant \tilde c$

    a lot of positive arguments to say $a \ S \ b$

  • (2) $d(a, b) \leqslant \tilde d$

    not many negative arguments to say the opposite

• so for that we also have to provide two parameters:
  • $\tilde c$ - the concordance threshold and $\tilde d$ - the discordance threshold

Or:

• $a \ S \ b \iff$
  • (1) $c(a, b) \geqslant \tilde c$
  • (2) $\forall g_i: \big(g_i(a), g_i(b)\big) \not \in D$

Note that this relation gives us partial order:

• we have $P$ and $I$ (expressed via $S$)
• and we have $J$ (when discordance threshold is exceeded)

Graph Kernels

Graph Kernels are used to identify good alternatives.

It is possible to express the outranking relation $S$ in form of a directed graph

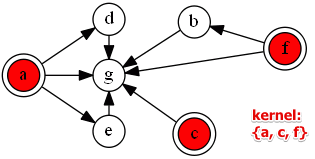
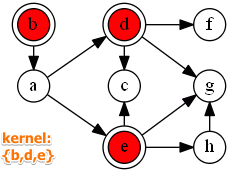
Example:

• 
• $a$ is better than $e$ and $d$
• $d$ is better than $f$ and $c$
• etc

A kernel of a graph $K \subset A$ is

• $\forall a \in K, \not \exists b: a \ S \ b$

  no alternative $a$ inside the kernel $K$ is better than any other alternative $b$ inside $K$

• $\forall a,b \in K: a \ ? \ b$

  within the kernel we cannot say anything about the relation between $a$ and $b$

• $\forall c \not \in K, \exists a \in K: a \ S \ c$

  each alternative $c$ outside of the kernel $K$ is worse than at least one alternative $a$ inside $K$

For the example above:

• $K = \{b, d, e\}$
• 

Another example

• 

Remarks:

• If the graph has no cycles then the kernel is unique
• Each cycle can be replaced by a single node (see Strongly Connected Components)

The kernel $K$ of a set $A$ forms a set of preferred alternatives.

Examples

Example 1

	price	comfort	speed	aesthetic
1	300	ex	fast	good
2	250	ex	med	good
3	250	med	fast	good
4	200	med	fast	med
5	200	med	med	good
7	100	poor	med	med
$w$	5	4	3	3	$W = \sum w = 15$

Concordance

Perform pair-wise comparisons for all elements $A$

• let's compare (1) and (2)
• concordance: $c(1, 2) = \cfrac{1}{15} (4 + 3 + 3) = \cfrac{2}{3}$

This way we compare each with each:

	1	2	3	4	5	6	7
1	-	10	10	10	10	10	10
2	12	-	12	7	10	7	10
3	11	11	-	10	10	10	10
4	8	8	12	-	12	12	10
5	8	11	12	12	-	12	10
6	11	11	11	11	11	-	10
7	5	8	5	8	8	9	-

(note that this is not normalized - need also to divide on 15)

Discordance

In this case we define discordance by enumerating cases that are forbidden

The following tables shows what veto we define

	price	comfort
$a$	250	poor
$b$	100	excellent

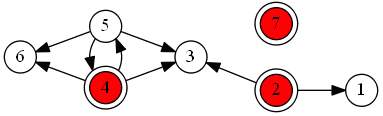
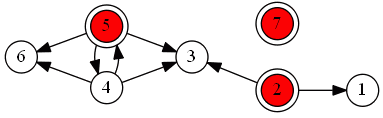
Graph

So the establish the following relation $S$ and the following graph:

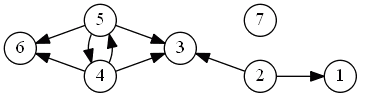
There are two kernels in this case:

• 2, 4, 7

  

• 2, 5, 7

  

Kernel:

• 6 is dominated - remove it
• same for 3 and 1
• since there's a cycle we have to decide between 4 and 5, and remove one of them
• when we put alternatives into a kernel, it doesn't mean they are the best, but it means it allows to apply the Dominance principle and remove dominated alternatives

Example 2

• A company wants to rank 5 candidates $A,B,C,D,E$ for a promotion
• Criteria:
  • Reputation of diploma $D$
  • Skills $K$
  • Personality $P$
  • Spoken Languages $L$
  • Seniority $S$
• Apply ELECTRE with concordance threshold 0.6 and discordance 6

The following evaluation table is obtained

	$A$	$B$	$C$	$D$	$E$	Weight
$D$	7	11	15	11	16	15
$K$	12	18	6	8	10	15
$P$	13	13	14	19	10	15
$L$	18	16	19	13	19	25
$S$	10	20	16	14	20	20

Total weight is $W = 15 + 15 + 15 + 25 + 20 = 100$

Concordance

Then we construct the concordance index by comparing alternatives pair-wise

For example, consider alternatives $A$ and $B$

	$A$ vs $B$	$B$ vs $A$
$D$		15
$K$		15
$P$	25	25
$L$	25
$S$		20
Total	50	100
Normalized	0.5	0.75

Repeating this for all pairs, construct the following table:

	$A$	$B$	$C$	$D$	$E$
$A$	-	0.75	0.15	0.4	0.4
$B$	0.5	-	0.35	0.75	0.6
$C$	0.85	0.65	-	0.6	0.5
$D$	0.6	0.25	0.4	-	0.25
$E$	0.6	0.6	0.75	0.75	-

Bold are alternatives that should be preferred provided that there's no discordance

• recall that $\tilde c = 0.6$ and we check all values that $\geqslant \tilde c$

Discordance

The discordance index is $\tilde d = 6$

• we don't normalize on $\delta$ here because our values are already normalized

Let's compare $A$ with $B$ and $A$ with $C$:

	$A$ vs $B$	$B$ vs $A$	$A$ vs $C$	$C$ vs $A$
$D$	7	-	8	-
$K$	6	-	-	6
$P$	0	0	1	-
$L$	-	2	1	-
$S$	10	-	6	-
Max	10	2	8	6
Rel	$A \ J \ B$		$A \ J \ C$	$C \ J \ A$

• if a difference exceeds the threshold, the alternatives are incomparable

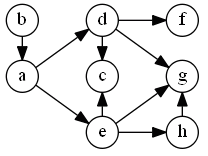
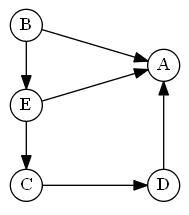
Graph

Based on the Concordance and Discordance we define the outranking relation $S$

• this relation can be depicted as a graph
• 

Sources

• Decision Engineering (ULB)
• http://web.itu.edu.tr/~topcuil/ya/MDM08Outranking.pptx
• http://electre.no.sapo.pt/MElecI2.htm
• Multiple Criteria Decision Analysis: State of the Art Surveys, 2005