Difference between revisions of "Translating SQL to Relational Algebra"
| Line 39: | Line 39: | ||
So we get: | So we get: | ||
| − | : | + | : <math>\pi_\text{movieTitle} \sigma_{\text{starName = M.name } \land \text{M.birthdate = 1960}}(\text{StartsIn} \times \rho_M (\text{MovieStar}))</math> |
(Maybe not the most efficient way, but it will be [[Logical Query Plan Optimization|optimized further]]) | (Maybe not the most efficient way, but it will be [[Logical Query Plan Optimization|optimized further]]) | ||
| Line 158: | Line 158: | ||
Algorithm | Algorithm | ||
* it's recursive: translate the subqueries first | * it's recursive: translate the subqueries first | ||
| − | ** | + | ** <math>\pi_\text{name} |
\sigma_{ | \sigma_{ | ||
\begin{subarray}{l} | \begin{subarray}{l} | ||
| Line 165: | Line 165: | ||
\end{subarray} | \end{subarray} | ||
} | } | ||
| − | (\text{MovieStar}) | + | (\text{MovieStar})</math> |
** problem: cannot find '''S.starName''' in the input relation | ** problem: cannot find '''S.starName''' in the input relation | ||
** so it must be a correlated query | ** so it must be a correlated query | ||
** we therefore need to recognize that this is a context relation's parameter | ** we therefore need to recognize that this is a context relation's parameter | ||
* so we need to add the context relations and parameters | * so we need to add the context relations and parameters | ||
| − | ** | + | ** <math>\pi_{ |
\begin{subarray}{l} | \begin{subarray}{l} | ||
\color{blue}{\text{S.movieTitle}}, \\ | \color{blue}{\text{S.movieTitle}}, \\ | ||
| Line 184: | Line 184: | ||
\end{subarray} | \end{subarray} | ||
} | } | ||
| − | (\text{MovieStar} {\color{red}{\times \rho_S(\text{StarsIn}) }}) | + | (\text{MovieStar} {\color{red}{\times \rho_S(\text{StarsIn}) }})</math> |
* next, we translate the "from" clause | * next, we translate the "from" clause | ||
** $\rho_S(\text{StarsIn}) \times \rho_M(\text{Movie})$ | ** $\rho_S(\text{StarsIn}) \times \rho_M(\text{Movie})$ | ||
| Line 190: | Line 190: | ||
** from the subquery we need to keep only the parameter attributes (the blue ones) - can remove $\text{name}$ | ** from the subquery we need to keep only the parameter attributes (the blue ones) - can remove $\text{name}$ | ||
** join: if something exists, we will join on it | ** join: if something exists, we will join on it | ||
| − | ** | + | ** <math>\big[ \rho_S(\text{StarsIn}) \times \rho_M(\text{Movie}) \big] |
\Join | \Join | ||
\big[ | \big[ | ||
| Line 207: | Line 207: | ||
} | } | ||
(\text{MovieStar} {\color{red}{\times \rho_S(\text{StarsIn}) }}) | (\text{MovieStar} {\color{red}{\times \rho_S(\text{StarsIn}) }}) | ||
| − | \big] | + | \big]</math> |
* note that we have $\rho_S(\text{StarsIn})$ on the both sides of the join | * note that we have $\rho_S(\text{StarsIn})$ on the both sides of the join | ||
** can just drop it (it won't affect the join) | ** can just drop it (it won't affect the join) | ||
| − | ** | + | ** <math>\big[ \rho_M(\text{Movie}) \big] |
\Join | \Join | ||
\big[ | \big[ | ||
| Line 227: | Line 227: | ||
} | } | ||
(\text{MovieStar}) | (\text{MovieStar}) | ||
| − | \big] | + | \big]</math> |
* finally we translate "WHERE" and "SELECT" | * finally we translate "WHERE" and "SELECT" | ||
| − | ** | + | ** <math>\pi_{ |
\begin{subarray}{l} | \begin{subarray}{l} | ||
\text{S.movieTitle}, \\ | \text{S.movieTitle}, \\ | ||
| Line 257: | Line 257: | ||
} | } | ||
(\text{MovieStar}) | (\text{MovieStar}) | ||
| − | \big] | + | \big]</math> |
| Line 275: | Line 275: | ||
Algorithm | Algorithm | ||
* Same as before: we translate the subquery | * Same as before: we translate the subquery | ||
| − | ** | + | ** <math>\pi_\text{name} |
\sigma_{ | \sigma_{ | ||
\begin{subarray}{l} | \begin{subarray}{l} | ||
| Line 282: | Line 282: | ||
\end{subarray} | \end{subarray} | ||
} | } | ||
| − | (\text{MovieStar}) | + | (\text{MovieStar})</math> |
* Then we add context relations and context parameters | * Then we add context relations and context parameters | ||
| − | ** | + | ** <math>\pi_{ |
\begin{subarray}{l} | \begin{subarray}{l} | ||
\color{blue}{\text{S.movieTitle}}, \\ | \color{blue}{\text{S.movieTitle}}, \\ | ||
| Line 298: | Line 298: | ||
\end{subarray} | \end{subarray} | ||
} | } | ||
| − | (\text{MovieStar} {\color{red}{\times \rho_S(\text{StarsIn}) }}) | + | (\text{MovieStar} {\color{red}{\times \rho_S(\text{StarsIn}) }})</math> |
* And same for the FROM clause | * And same for the FROM clause | ||
** $\rho_S(\text{StarsIn}) \times \rho_M(\text{Movie})$ | ** $\rho_S(\text{StarsIn}) \times \rho_M(\text{Movie})$ | ||
* Then we need to ''synchronize'' the results, but this time with [[Relational Algebra#Anti-Join|Anti-Join]] ($\AntiJoin$) | * Then we need to ''synchronize'' the results, but this time with [[Relational Algebra#Anti-Join|Anti-Join]] ($\AntiJoin$) | ||
| − | ** | + | ** <math>\big[ \rho_S(\text{StarsIn}) \times \rho_M(\text{Movie}) \big] |
\AntiJoin | \AntiJoin | ||
\big[ | \big[ | ||
| Line 319: | Line 319: | ||
} | } | ||
(\text{MovieStar} \times \rho_S(\text{StarsIn}) ) | (\text{MovieStar} \times \rho_S(\text{StarsIn}) ) | ||
| − | \big] | + | \big]</math> |
** note that here the simplification is not possible: the semantics of Anti-Join is different from Join | ** note that here the simplification is not possible: the semantics of Anti-Join is different from Join | ||
** so we cannot remove $\rho_S(\text{StarsIn})$ from both parts | ** so we cannot remove $\rho_S(\text{StarsIn})$ from both parts | ||
* the last step is the same: we translate "WHERE" and "SELECT" | * the last step is the same: we translate "WHERE" and "SELECT" | ||
| − | ** | + | ** <math>\pi_{ |
\begin{subarray}{l} | \begin{subarray}{l} | ||
\text{S.movieTitle}, \\ | \text{S.movieTitle}, \\ | ||
| Line 354: | Line 354: | ||
(\text{MovieStar} \times \rho_S(\text{StarsIn}) ) | (\text{MovieStar} \times \rho_S(\text{StarsIn}) ) | ||
\big] | \big] | ||
| − | \bigg] | + | \bigg]</math> |
| − | + | ||
| Line 422: | Line 422: | ||
* and make sure that they have the same name | * and make sure that they have the same name | ||
| − | + | <math>\bigg( | |
\underbrace{ | \underbrace{ | ||
\pi_{ | \pi_{ | ||
| Line 453: | Line 453: | ||
\big[\rho_{R_1}(R) \times \rho_{S_1}(S) {\color{blue} \times \rho_{S_2}(S) } \big] | \big[\rho_{R_1}(R) \times \rho_{S_1}(S) {\color{blue} \times \rho_{S_2}(S) } \big] | ||
}_{(2)} | }_{(2)} | ||
| − | \bigg) | + | \bigg)</math> |
| − | + | ||
| Line 476: | Line 476: | ||
We translate it as | We translate it as | ||
| − | * | + | * <math>\pi_{ |
\begin{subarray}{l} | \begin{subarray}{l} | ||
\text{name}, \\ | \text{name}, \\ | ||
| Line 483: | Line 483: | ||
} | } | ||
{\color{blue} | {\color{blue} | ||
| − | \sigma_{\text{MIN(year) < 1930 | + | \sigma_{\text{MIN(year)} < 1930} |
\gamma_{ | \gamma_{ | ||
\begin{subarray}{l} | \begin{subarray}{l} | ||
| Line 493: | Line 493: | ||
} | } | ||
\sigma_{\text{cert = producer}} | \sigma_{\text{cert = producer}} | ||
| − | (\text{MovieExec} \times \text{Movie}) | + | (\text{MovieExec} \times \text{Movie})</math> |
* here the translate the '''HAVING''' clause as $\sigma$ before the $\gamma$ | * here the translate the '''HAVING''' clause as $\sigma$ before the $\gamma$ | ||
| Line 556: | Line 556: | ||
Now we translate the subquery | Now we translate the subquery | ||
| − | * | + | * <math>q_1 = |
\pi_{\text{E.name, C.*}} | \pi_{\text{E.name, C.*}} | ||
\sigma_{\text{cat} \geqslant 5} | \sigma_{\text{cat} \geqslant 5} | ||
| Line 569: | Line 569: | ||
\big( | \big( | ||
\rho_E(\text{Enrolled}) \times \rho_C(\text{Class}) | \rho_E(\text{Enrolled}) \times \rho_C(\text{Class}) | ||
| − | \big) | + | \big)</math> |
| − | + | ||
| − | * '''note''' that we use | + | * '''note''' that we use <math>\gamma_{ |
\begin{subarray}{l} | \begin{subarray}{l} | ||
\text{E.cname}, \\ | \text{E.cname}, \\ | ||
| Line 577: | Line 577: | ||
\text{C.*} | \text{C.*} | ||
\end{subarray} | \end{subarray} | ||
| − | } | + | }</math> and not <math>\gamma_{ |
\begin{subarray}{l} | \begin{subarray}{l} | ||
\text{E.cname}, \\ | \text{E.cname}, \\ | ||
\text{count(*) $\to$ cnt} | \text{count(*) $\to$ cnt} | ||
\end{subarray} | \end{subarray} | ||
| − | } | + | }</math>, because in the second case it will return only the two specified columns |
Next, we need to synchronize (or "decorrelate") the subquery $q_1$ and the outer query | Next, we need to synchronize (or "decorrelate") the subquery $q_1$ and the outer query | ||
| − | * | + | * <math> |
\pi_{\text{C.name}} | \pi_{\text{C.name}} | ||
\Big[ | \Big[ | ||
| Line 604: | Line 604: | ||
\rho_E(\text{Enrolled}) \times \rho_C(\text{Class}) | \rho_E(\text{Enrolled}) \times \rho_C(\text{Class}) | ||
\big) | \big) | ||
| − | \Big] | + | \Big]</math> |
| − | + | ||
* add $\pi_{\text{C.*}}$ because we need only these values - '''E.name''' was used for EXISTS part only | * add $\pi_{\text{C.*}}$ because we need only these values - '''E.name''' was used for EXISTS part only | ||
* since we have $\rho_C(\text{Class})$ on both sides of the Join - we can drop the first one (as well as the Join) | * since we have $\rho_C(\text{Class})$ on both sides of the Join - we can drop the first one (as well as the Join) | ||
* and we also can merge successive projections | * and we also can merge successive projections | ||
* so we get: | * so we get: | ||
| − | * | + | * <math>\pi_{\text{C.name}} |
\sigma_{\text{cat} \geqslant 5} | \sigma_{\text{cat} \geqslant 5} | ||
\gamma_{ | \gamma_{ | ||
| Line 622: | Line 622: | ||
\big( | \big( | ||
\rho_E(\text{Enrolled}) \times \rho_C(\text{Class}) | \rho_E(\text{Enrolled}) \times \rho_C(\text{Class}) | ||
| − | \big) | + | \big)</math> |
| Line 628: | Line 628: | ||
* Since both parts have the same schema, union is possible | * Since both parts have the same schema, union is possible | ||
* The total results is: | * The total results is: | ||
| − | * | + | * <math> |
\pi_\text{C.name} \sigma_\text{C.room = 'R128'} | \pi_\text{C.name} \sigma_\text{C.room = 'R128'} | ||
\rho_C(\text{Class}) | \rho_C(\text{Class}) | ||
| Line 644: | Line 644: | ||
\big( | \big( | ||
\rho_E(\text{Enrolled}) \times \rho_C(\text{Class}) | \rho_E(\text{Enrolled}) \times \rho_C(\text{Class}) | ||
| − | \big) | + | \big)</math> |
| − | + | ||
=== Exercise with the Count Bug === | === Exercise with the Count Bug === | ||
| Line 678: | Line 678: | ||
Using the rules, we try to translate the query this way: | Using the rules, we try to translate the query this way: | ||
* first we translate the subquery | * first we translate the subquery | ||
| − | ** | + | ** <math> |
\pi_{ | \pi_{ | ||
\begin{subarray}{l} | \begin{subarray}{l} | ||
| Line 687: | Line 687: | ||
\end{subarray} | \end{subarray} | ||
} | } | ||
| − | \sigma_\text{cnt < 5} | + | \sigma_{\text{cnt} < 5} |
\gamma_{ | \gamma_{ | ||
\begin{subarray}{l} | \begin{subarray}{l} | ||
| Line 702: | Line 702: | ||
\Big[ | \Big[ | ||
\rho_C(\text{Class}) \times \rho_E(\text{Enrolled}) \times \rho_F(\text{Faculty}) | \rho_C(\text{Class}) \times \rho_E(\text{Enrolled}) \times \rho_F(\text{Faculty}) | ||
| − | \Big] | + | \Big]</math> |
| − | + | ||
* then decorrelate it: | * then decorrelate it: | ||
| − | ** | + | ** <math> |
\rho_F(\text{Faculty}) | \rho_F(\text{Faculty}) | ||
\Join | \Join | ||
| Line 718: | Line 717: | ||
\end{subarray} | \end{subarray} | ||
} | } | ||
| − | \sigma_\text{cnt < 5} | + | \sigma_{\text{cnt} < 5} |
\gamma_{ | \gamma_{ | ||
\begin{subarray}{l} | \begin{subarray}{l} | ||
| Line 734: | Line 733: | ||
\rho_C(\text{Class}) \times \rho_E(\text{Enrolled}) \times \rho_F(\text{Faculty}) | \rho_C(\text{Class}) \times \rho_E(\text{Enrolled}) \times \rho_F(\text{Faculty}) | ||
\Big] | \Big] | ||
| − | \bigg) | + | \bigg)</math> |
| − | + | ||
* can remove $\rho_F(\text{Faculty})$ and keep only needed projection attributes | * can remove $\rho_F(\text{Faculty})$ and keep only needed projection attributes | ||
| − | ** | + | ** <math>\pi_{\text{F.name}} |
| − | \sigma_\text{cnt < 5} | + | \sigma_{\text{cnt} < 5} |
\gamma_{ | \gamma_{ | ||
\begin{subarray}{l} | \begin{subarray}{l} | ||
| Line 753: | Line 751: | ||
\Big[ | \Big[ | ||
\rho_C(\text{Class}) \times \rho_E(\text{Enrolled}) \times \rho_F(\text{Faculty}) | \rho_C(\text{Class}) \times \rho_E(\text{Enrolled}) \times \rho_F(\text{Faculty}) | ||
| − | \Big] | + | \Big]</math> |
Note that this is '''not the query we want'''!!! | Note that this is '''not the query we want'''!!! | ||
| Line 764: | Line 762: | ||
* to solve it we need to use right outer join instead of $\times$ | * to solve it we need to use right outer join instead of $\times$ | ||
| − | + | <math>\pi_{\text{F.name}} | |
| − | \sigma_\text{cnt < 5} | + | \sigma_{\text{cnt} < 5} |
\gamma_{ | \gamma_{ | ||
\begin{subarray}{l} | \begin{subarray}{l} | ||
| Line 780: | Line 778: | ||
\Big[ | \Big[ | ||
\rho_C(\text{Class}) \times \rho_E(\text{Enrolled}) \Join^{R}_\text{C.fid = F.fid} \rho_F(\text{Faculty}) | \rho_C(\text{Class}) \times \rho_E(\text{Enrolled}) \Join^{R}_\text{C.fid = F.fid} \rho_F(\text{Faculty}) | ||
| − | \Big] | + | \Big]</math> |
Latest revision as of 22:46, 14 August 2018
\(\require{color}\) \(\newcommand{\AntiJoin}{ \ \bar{\Join} \ } \)
Contents
Translating SQL to Relational Algebra
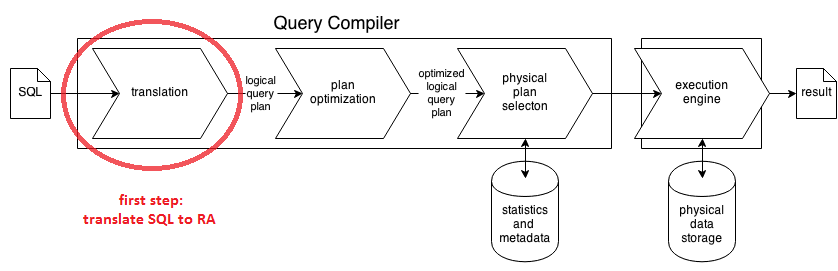
Translating SQL to RA expression is the second step in Query Processing Pipeline
- Input: Logical Query Plan - expression in Extended Relational Algebra
- Output: Optimized Logical Query Plan - also in Relational Algebra
Union, Intersection, Difference
Translation is straightforward
(SELECT * FROM R1) INTERSECT (SELECT * FROM R2)
Is $R_1 \cap R_2$
UNION $\to R_1 \cup R_2$
EXCEPT $\to R_1 - R_2$
Select-From-Where No Subqueries
Query
SELECT movieTitle FROM StarsIn, MovieStarM WHERE starName = M.name AND M.birthdate = 1960
- in the from clause we have all relations we need
- so we make a Cartesian Product for all relations there
- if there is an alias - we do Renaming
- then we filter the Cartesian Product
- then translate the where clause too
So we get:
- [math]\pi_\text{movieTitle} \sigma_{\text{starName = M.name } \land \text{M.birthdate = 1960}}(\text{StartsIn} \times \rho_M (\text{MovieStar}))[/math]
(Maybe not the most efficient way, but it will be optimized further)
Normalization Step
Suppose we have subqueries in the "Where" clause
SELECT movieTitle FROM StarsIn
WHERE starName IN (
SELECT name
FROM MovieStar
WHERE birthdate=1960)
Here we may have different constraints:
- $\text{in}, \leqslant, <, \geqslant, >, =, \neq$, etc
- whenever we have such constraints, we may replace them with quantifiers $\forall$ and $\exists$
- or with EXISTS and IN or NOT EXISTS
- so we first translate a SQL query to the equivalent SQL with EXISTS or NOT EXISTS
Example 1: IN
SELECT movieTitle FROM StarsIn
WHERE starName IN (
SELECT name
FROM MovieStar
WHERE birthdate=1960)
to
SELECT movieTitle FROM StarsIn
WHERE EXISTS (
SELECT name
FROM MovieStar
WHERE birthdate=1960 AND name=starName)
Example 2: $\geqslant$
SELECT name FROM MovieExec
WHERE netWorth >= (
SELECT E.netWorth
FROM MovieExec E)
to
SELECT name FROM MovieExec
WHERE NOT EXISTS (
SELECT E.netWorth
FROM MovieExec E
WHERE netWorth < E.netWorth)
Example 3: aggregated attributes
SELECT C FROM S
WHERE C IN (
SELECT SUM(B) FROM R
GROUP BY A)
to
SELECT C FROM S
WHERE EXISTS (
SELECT SUM(B) FROM R
GROUP BY A
HAVING SUM(B) = C)
(note that in this case we use "HAVING" and not "WHERE")
So the first step when processing these kinds of queries is normalization step:
- translate a query into EXISTS/NOT EXISTS form
Hence we can assume that all queries are in this form
- We then apply the next step: for correlated queries
- A subquery can refer to attributes of relations that are introduces in the outer query
- def: we call such queries correlated subqueries
- the outer relation is called the context relation - a correlated subquery uses its attributes
- a parameter - is a set of attributes of all context relations of a subquery
Example:

here
- the subquery refers to S.starName, so it's correlated
- S is the context relation for the subquery
- S.starName is a parameter to the correlated subquery
EXISTS in the Where Clause (by example)
SELECT S.movieTitle, M.studioName
FROM StarsIn S, Movie M
WHERE S.movieYear >= 2000
AND S.movieTitle = M.title
AND EXISTS (
SELECT name
FROM MovieStar
WHERE birthdate = 1960 AND name = S.starName)
Algorithm
- it's recursive: translate the subqueries first
- [math]\pi_\text{name} \sigma_{ \begin{subarray}{l} \text{birthDate = 1960 } \land \\ \text{name = S.starName} \\ \end{subarray} } (\text{MovieStar})[/math]
- problem: cannot find S.starName in the input relation
- so it must be a correlated query
- we therefore need to recognize that this is a context relation's parameter
- so we need to add the context relations and parameters
- [math]\pi_{ \begin{subarray}{l} \color{blue}{\text{S.movieTitle}}, \\ \color{blue}{\text{S.movieYear}}, \\ \color{blue}{\text{S.starName}}, \\ \text{name} \\ \end{subarray} } \sigma_{ \begin{subarray}{l} \text{birthDate = 1960 } \land \\ \text{name = S.starName} \\ \end{subarray} } (\text{MovieStar} {\color{red}{\times \rho_S(\text{StarsIn}) }})[/math]
- next, we translate the "from" clause
- $\rho_S(\text{StarsIn}) \times \rho_M(\text{Movie})$
- now we need to synchronize the subresult by join
- from the subquery we need to keep only the parameter attributes (the blue ones) - can remove $\text{name}$
- join: if something exists, we will join on it
- [math]\big[ \rho_S(\text{StarsIn}) \times \rho_M(\text{Movie}) \big] \Join \big[ \pi_{ \begin{subarray}{l} \color{blue}{\text{S.movieTitle}}, \\ \color{blue}{\text{S.movieYear}}, \\ \color{blue}{\text{S.starName}} \end{subarray} } \sigma_{ \begin{subarray}{l} \text{birthDate = 1960 } \land \\ \text{name = S.starName} \\ \end{subarray} } (\text{MovieStar} {\color{red}{\times \rho_S(\text{StarsIn}) }}) \big][/math]
- note that we have $\rho_S(\text{StarsIn})$ on the both sides of the join
- can just drop it (it won't affect the join)
- [math]\big[ \rho_M(\text{Movie}) \big] \Join \big[ \pi_{ \begin{subarray}{l} \text{S.movieTitle}, \\ \text{S.movieYear}, \\ \text{S.starName} \end{subarray} } \sigma_{ \begin{subarray}{l} \text{birthDate = 1960 } \land \\ \text{name = S.starName} \\ \end{subarray} } (\text{MovieStar}) \big][/math]
- finally we translate "WHERE" and "SELECT"
- [math]\pi_{ \begin{subarray}{l} \text{S.movieTitle}, \\ \text{M.studioName} \end{subarray} } \sigma_{ \begin{subarray}{l} \text{S.movieYear $\geqslant$ 2000 } \land \\ \text{S.movieTitle = M.title} \\ \end{subarray} } \big[ \rho_M(\text{Movie}) \Join \pi_{ \begin{subarray}{l} \text{S.movieTitle}, \\ \text{S.movieYear}, \\ \text{S.starName} \end{subarray} } \sigma_{ \begin{subarray}{l} \text{birthDate = 1960 } \land \\ \text{name = S.starName} \\ \end{subarray} } (\text{MovieStar}) \big][/math]
NOT EXISTS in the Where Clause (by example)
SELECTS.movieTitle, M.studioName
FROM StarsIn S, Movie M
WHERE S.movieYear >= 2000
AND S.movieTitle = M.title
AND NOT EXISTS (
SELECT name
FROM MovieStar
WHERE birthdate = 1960 AND name = S.starName)
Algorithm
- Same as before: we translate the subquery
- [math]\pi_\text{name} \sigma_{ \begin{subarray}{l} \text{birthDate = 1960 } \land \\ \text{name = S.starName} \\ \end{subarray} } (\text{MovieStar})[/math]
- Then we add context relations and context parameters
- [math]\pi_{ \begin{subarray}{l} \color{blue}{\text{S.movieTitle}}, \\ \color{blue}{\text{S.movieYear}}, \\ \color{blue}{\text{S.starName}}, \\ \text{name} \\ \end{subarray} } \sigma_{ \begin{subarray}{l} \text{birthDate = 1960 } \land \\ \text{name = S.starName} \\ \end{subarray} } (\text{MovieStar} {\color{red}{\times \rho_S(\text{StarsIn}) }})[/math]
- And same for the FROM clause
- $\rho_S(\text{StarsIn}) \times \rho_M(\text{Movie})$
- Then we need to synchronize the results, but this time with Anti-Join ($\AntiJoin$)
- [math]\big[ \rho_S(\text{StarsIn}) \times \rho_M(\text{Movie}) \big] \AntiJoin \big[ \pi_{ \begin{subarray}{l} \text{S.movieTitle}, \\ \text{S.movieYear}, \\ \text{S.starName} \end{subarray} } \sigma_{ \begin{subarray}{l} \text{birthDate = 1960 } \land \\ \text{name = S.starName} \\ \end{subarray} } (\text{MovieStar} \times \rho_S(\text{StarsIn}) ) \big][/math]
- note that here the simplification is not possible: the semantics of Anti-Join is different from Join
- so we cannot remove $\rho_S(\text{StarsIn})$ from both parts
- the last step is the same: we translate "WHERE" and "SELECT"
- [math]\pi_{ \begin{subarray}{l} \text{S.movieTitle}, \\ \text{M.studioName} \end{subarray} } \sigma_{ \begin{subarray}{l} \text{S.movieYear $\geqslant$ 2000 } \land \\ \text{S.movieTitle = M.title} \\ \end{subarray} } \bigg[ \big[ \rho_S(\text{StarsIn}) \times \rho_M(\text{Movie}) \big] \AntiJoin \big[ \pi_{ \begin{subarray}{l} \text{S.movieTitle}, \\ \text{S.movieYear}, \\ \text{S.starName} \end{subarray} } \sigma_{ \begin{subarray}{l} \text{birthDate = 1960 } \land \\ \text{name = S.starName} \\ \end{subarray} } (\text{MovieStar} \times \rho_S(\text{StarsIn}) ) \big] \bigg][/math]
EXISTS Subqueries in WHERE Combined with Other
So far we've considered only queries of the following form:
SELECT ... FROM ...
WHERE ... AND
EXISTS (...) AND
... AND
NOT EXISTS (...)
I.e. EXISTS and NOT EXISTS are in the "WHERE" clause joined by "AND"
What about the following query?
SELECT ... FROM ...
WHERE
A = B AND NOT (EXISTS (...) AND C < 6)
- First, we translate the condition into Disjunctive Normal Form
SELECT ... FROM ...
WHERE
(A = B AND NOT (EXISTS (...))) OR
(A = B AND C >= 6)
- Then we distribute OR (to UNION)
(SELECT ... FROM ...
WHERE
A = B AND NOT EXISTS (...))
UNION
(SELECT ... FROM ...
WHERE
A = B AND C >= 6)
As we've seen, UNION is translated as $\cup$
Union In Subqueries
We may have UNOIN in subqueries
SELECT S1.C, S2.C FROM S S1, S S2 WHERE EXISTS ( (SELECT R1.A, R1.B FROMR R1 WHERE A = S1.C AND B = S2.C) -- (1) UNION (SELECT R2.A, R2.B FROMR R2 WHERE B = S1.C) -- (2) )
- Recall that to be able to UNION two relations, they must have the same schema
- But in this case:
- (1) has 2 context relations $S_1$ and $S_2$
- (2) has only 1 context relation $S_1$
- $\Rightarrow$ When translating, need to add $S_2$ to (2) as well
- and make sure that they have the same name
[math]\bigg( \underbrace{ \pi_{ \begin{subarray}{l} S_1.C, \ S_2.C, \\ R_1.A \ {\color{blue} \to \ A}, \\ R_1.B \ {\color{blue} \to \ B} \end{subarray} } \sigma_{ \begin{subarray}{l} A = S_1.C \ \land \\ B = S_2.C \\ \end{subarray} } \big[\rho_{R_1}(R) \times \rho_{S_1}(S) \times \rho_{S_2}(S) \big] }_{(1)} \bigg) \ {\color{blue} \cup } \ \bigg( \underbrace{ \pi_{ \begin{subarray}{l} S_1.C, \ S_2.C, \\ R_1.A \ {\color{blue} \to \ A}, \\ R_1.B \ {\color{blue} \to \ B} \end{subarray} } \sigma_{B = S_1.C} \big[\rho_{R_1}(R) \times \rho_{S_1}(S) {\color{blue} \times \rho_{S_2}(S) } \big] }_{(2)} \bigg)[/math]
Translating Joins
Joins
(SELECT * FROM R R1) JOIN (SELECT * FROM R R1) ON R1.A = R2.B
We translate as follows:
- $\rho_{R_1}(R) \Join_{R_1.A = R_2.B} \rho_{R_2}(R)$
Group and Having
Suppose we have the following query:
SELECT name, SUM(length) FROM MovieExec, Movie WHERE cert = producer GROUP BY name HAVING MIN(year) < 1930
We translate it as
- [math]\pi_{ \begin{subarray}{l} \text{name}, \\ \text{SUM(length)} \end{subarray} } {\color{blue} \sigma_{\text{MIN(year)} \lt 1930} \gamma_{ \begin{subarray}{l} \text{name}, \\ \text{MIN(year)}, \\ \text{SUM(length)} \end{subarray} } } \sigma_{\text{cert = producer}} (\text{MovieExec} \times \text{Movie})[/math]
- here the translate the HAVING clause as $\sigma$ before the $\gamma$
- also note that SUM(length) goes to $\gamma$
Exercises
Exercises from Database Systems Architecture (ULB)
Exercise 1
The given relations:
- Student(snum, sname, major, level, age)
- Class(name, meets_at, room, fid)
- Enrolled(snum, cname)
- Faculty(fid, fname, deptid)
SELECT C.name
FROM Class C
WHERE C.room = 'R128' OR
C.name IN (
SELECT E.cname
FROM Enrolled E
GROUP BY E.cname
HAVING COUNT(*) >= 5)
First we distribute OR
SELECT C.name
FROM Class C
WHERE C.room = 'R128'
UNION
SELECT C.name
FROM Class C
WHERE C.name IN (
SELECT E.cname
FROM Enrolled E
GROUP BY E.cname
HAVING COUNT(*) >= 5)
for the subquery we replace IN to EXISTS
SELECT C.name
FROM Class C
WHERE EXISTS (
SELECT E.cname
FROM Enrolled E
WHERE E.cname = C.name
GROUP BY E.cname
HAVING COUNT(*) >= 5)
Now we translate the subquery
- [math]q_1 = \pi_{\text{E.name, C.*}} \sigma_{\text{cat} \geqslant 5} \gamma_{ \begin{subarray}{l} \text{E.cname}, \\ \text{count(*) $\to$ cnt}, \\ \text{C.*} \end{subarray} } \sigma_{\text{E.cname = C.name}} \big( \rho_E(\text{Enrolled}) \times \rho_C(\text{Class}) \big)[/math]
- note that we use [math]\gamma_{ \begin{subarray}{l} \text{E.cname}, \\ \text{count(*) $\to$ cnt}, \\ \text{C.*} \end{subarray} }[/math] and not [math]\gamma_{ \begin{subarray}{l} \text{E.cname}, \\ \text{count(*) $\to$ cnt} \end{subarray} }[/math], because in the second case it will return only the two specified columns
Next, we need to synchronize (or "decorrelate") the subquery $q_1$ and the outer query
- [math] \pi_{\text{C.name}} \Big[ \rho_C(\text{Class}) \Join \pi_{\text{C.*}} \pi_{\text{E.name, C.*}} \sigma_{\text{cat} \geqslant 5} \gamma_{ \begin{subarray}{l} \text{E.cname}, \\ \text{count(*) $\to$ cnt}, \\ \text{C.*} \end{subarray} } \sigma_{\text{E.cname = C.name}} \big( \rho_E(\text{Enrolled}) \times \rho_C(\text{Class}) \big) \Big][/math]
- add $\pi_{\text{C.*}}$ because we need only these values - E.name was used for EXISTS part only
- since we have $\rho_C(\text{Class})$ on both sides of the Join - we can drop the first one (as well as the Join)
- and we also can merge successive projections
- so we get:
- [math]\pi_{\text{C.name}} \sigma_{\text{cat} \geqslant 5} \gamma_{ \begin{subarray}{l} \text{E.cname}, \\ \text{count(*) $\to$ cnt}, \\ \text{C.*} \end{subarray} } \sigma_{\text{E.cname = C.name}} \big( \rho_E(\text{Enrolled}) \times \rho_C(\text{Class}) \big)[/math]
Now we do the union (easy)
- Since both parts have the same schema, union is possible
- The total results is:
- [math] \pi_\text{C.name} \sigma_\text{C.room = 'R128'} \rho_C(\text{Class}) \cup \pi_{\text{C.name}} \sigma_{\text{cat} \geqslant 5} \gamma_{ \begin{subarray}{l} \text{E.cname}, \\ \text{count(*) $\to$ cnt}, \\ \text{C.*} \end{subarray} } \sigma_{\text{E.cname = C.name}} \big( \rho_E(\text{Enrolled}) \times \rho_C(\text{Class}) \big)[/math]
Exercise with the Count Bug
SELECT F.fname
FROM Faculty F
WHERE 5 > (
SELECT COUNT(E.snum)
FROM Class C, Enrolled E
WHERE C.name = E.cname AND
C.fid = F.fid)
First translate to an equivalent EXISTS query
SELECT F.fname
FROM Faculty F
WHERE EXISTS (
SELECT COUNT(E.snum) as CNT
FROM Class C, Enrolled E
WHERE C.name = E.cname AND
C.fid = F.fid
HAVING CNT < 5)
Remarks
- note the change in the sign from > to <
- also we use HAVING instead of WHERE - because GROUP is assumed
- not all databases will take this kind of query.
- For instance, MySQL will not (however it's not fully SQL compliant)
Using the rules, we try to translate the query this way:
- first we translate the subquery
- [math] \pi_{ \begin{subarray}{l} \text{cnt)}, \\ \text{F.fid}, \\ \text{F.fname}, \\ \text{F.deptid} \end{subarray} } \sigma_{\text{cnt} \lt 5} \gamma_{ \begin{subarray}{l} \text{count(E.snum) $\to$ cnt}, \\ \text{F.*} \end{subarray} } \sigma_{ \begin{subarray}{l} \text{C.name = E.cname } \land \\ \text{C.fid = F.fid} \end{subarray} } \Big[ \rho_C(\text{Class}) \times \rho_E(\text{Enrolled}) \times \rho_F(\text{Faculty}) \Big][/math]
- then decorrelate it:
- [math] \rho_F(\text{Faculty}) \Join \bigg( \pi_{\text{F.*}} \pi_{ \begin{subarray}{l} \text{cnt}, \\ \text{F.fid}, \\ \text{F.fname}, \\ \text{F.deptid} \end{subarray} } \sigma_{\text{cnt} \lt 5} \gamma_{ \begin{subarray}{l} \text{count(E.snum) $\to$ cnt}, \\ \text{F.*} \end{subarray} } \sigma_{ \begin{subarray}{l} \text{C.name = E.cname } \land \\ \text{C.fid = F.fid} \end{subarray} } \Big[ \rho_C(\text{Class}) \times \rho_E(\text{Enrolled}) \times \rho_F(\text{Faculty}) \Big] \bigg)[/math]
- can remove $\rho_F(\text{Faculty})$ and keep only needed projection attributes
- [math]\pi_{\text{F.name}} \sigma_{\text{cnt} \lt 5} \gamma_{ \begin{subarray}{l} \text{count(E.snum) $\to$ cnt}, \\ \text{F.*} \end{subarray} } \sigma_{ \begin{subarray}{l} \text{C.name = E.cname } \land \\ \text{C.fid = F.fid} \end{subarray} } \Big[ \rho_C(\text{Class}) \times \rho_E(\text{Enrolled}) \times \rho_F(\text{Faculty}) \Big][/math]
Note that this is not the query we want!!!
- Faculty members who don't teach any class are not output by the expression, but they are output by the original SQL query
Count bug
- this issue is known as the count bug
- it occurs when we have subqueries use COUNT without GROUP BY
- to solve it we need to use right outer join instead of $\times$
[math]\pi_{\text{F.name}} \sigma_{\text{cnt} \lt 5} \gamma_{ \begin{subarray}{l} \text{count(E.snum) $\to$ cnt}, \\ \text{F.*} \end{subarray} } \sigma_{ \begin{subarray}{l} \text{C.name = E.cname } \land \\ \text{C.fid = F.fid} \end{subarray} } \Big[ \rho_C(\text{Class}) \times \rho_E(\text{Enrolled}) \Join^{R}_\text{C.fid = F.fid} \rho_F(\text{Faculty}) \Big][/math]
See also
- Relational Algebra
- Lecture Notes by S. Vansummeren [3]