Basis (Linear Algebra)
In Linear Algebra, ‘‘basis’’ is a set of linearly independent vectors $\mathbf v_1, …, \mathbf v_n$
Spanning a Space
Vectors $\mathbf v_1, …, \mathbf v_l$ ‘‘span a (sub)space’’ $\iff$ this space consists of all possible linear combinations of these vectors
- columns of a matrix $A$ span it’s column space $C(A)$
- are such $\mathbf v_i$ independent? - depends
Basis
Basis of a vector space is a sequence of vectors $\mathbf v_1, \mathbf v_2, …, \mathbf v_d$ that
- are linearly independent and
- span the entire space
Examples
Standard Basis:
- the identity $I_d$,
- e.g. for $\mathbb R^3$, $\mathbf e_1 = \begin{bmatrix} 1 \ 0 \ 0 \end{bmatrix}$, $\mathbf e_2 = \begin{bmatrix} 0 \ 1 \ 0 \end{bmatrix}$, $\mathbf e_3 = \begin{bmatrix} 0 \ 0 \ 1 \end{bmatrix}$
Non-Example:
- $\begin{bmatrix} 1 \ 1 \ 2 \end{bmatrix}$, $\begin{bmatrix} 2 \ 2 \ 5 \end{bmatrix}$, linearly independent, but don’t span $\mathbb R^3$
- $\begin{bmatrix} 1 \ 1 \ 2 \end{bmatrix}$, $\begin{bmatrix} 2 \ 2 \ 5 \end{bmatrix}$, $\begin{bmatrix} 3 \ 3 \ 7 \end{bmatrix}$, the 3rd vector is a linear combination of first 2
- the first case is 2 vectors on a plane, and 2nd is 3 vectors on a plane
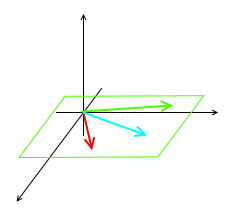
Another example:
- $\begin{bmatrix} 1 \ 1 \ 2 \end{bmatrix}$, $\begin{bmatrix} 2 \ 2 \ 5 \end{bmatrix}$, $\begin{bmatrix} 3 \ 1 \ 8 \end{bmatrix}$
- if we put the vectors as columns of a matrix, then the rank should be equal to the number of vectors
- $\begin{bmatrix}
1 & 2 & 3
1 & 2 & 1\ 2 & 5 & 8
\end{bmatrix}$, rank is 3
Also,
- take any invertible $n \times n$ matrix, take the columns from it and get a basis
Dimension
Every space has some basis, and each basis of this space has the same number of vectors. The number of vectors in the basis is the ‘‘dimension’’ of this space.