Linear Independence
Vectors $\mathbf x_1, \mathbf x_2, … , \mathbf x_n$ are ‘‘linearly independent’’ if no linear combinations gives a zero vector $\mathbf 0$
- $c_1 \mathbf x_1 + c_2 \mathbf x_2 + … + c_n \mathbf x_n \ne \mathbf 0$
- only when $\forall i: c_i = 0$ it’s true that $\sum c_i \mathbf x_i = 0$
Examples
Example 1
- suppose we have a vector $v_1$ and a vector $v_2 = c \cdot v_1$

- this system is dependent
Zero vector always means a dependence
- suppose we have vector $v_1 \ne \mathbf 0$ and $v_2 = \mathbf 0$
- $0 \mathbf v_1 + c \mathbf v_2 = \mathbf 0$ for any $c$
Example 2
- suppose we have a system of two independent vectors $v_1$ and $v_2$ in $\mathbb R^2$

- what happens if we add 3rd vectors $v_3$?
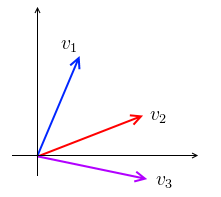
- the system is no longer dependent - we always can express $v_3$ in terms of $v_1$ and $v_2$ and when we add them, we’ll have 0
- so if the number of vectors is greater than the dimensionality of these vectors, the system cannot be independent
Matrices
Columns of a matrix $A$ are independent if the Nullspace $N(A)$ contains only $\mathbf 0$
- otherwise the columns are dependents
- Why? recall that $N(A)$ contains the solutions to the system $A\mathbf x = \mathbf 0$
- so there’s a combination of columns with coefficients $\mathbf x$ that is equal to $\mathbf 0$
- It’s related to rank as well:
- if $r = n$, then there are no free variables and $N(A) = { \, \mathbf 0 \, }$
-
if $r < n$, there are free variables and $ N(A) > 1$