Constraint-Based Pattern Mining
Goal:
- to enumerate all patterns that satisfy some constraint $q$
- $q \equiv m(X, D) \geqslant \text{threshold}$
- so it’s a general case of Frequent Pattern Mining
- where constraint is $\text{freq}(X, D) \geqslant \text{min_frec}$
Example
Example:
- suppose $q \equiv \sum_{x \in X} x.\text{price} \leqslant 8$
- prices: $(a \to 1, b \to 2, c \to 5, d \to 4, e \to 6, f \to 4)$
- the same idea as in Frequent Pattern Mining
- enumerate all subsets, check ones in which this constraint is satisfied
- solution:
- $({} \to 0), (a \to 1), (b \to 2), (c \to 5), (d \to 4), (e \to 6),$
- $(f \to 4), (ab \to 3), (ac \to 6), (ad \to 5), (ae \to 7), (af \to 5),$
- $(bc \to 7), (bd \to 6), (be \to 8), (bf \to 6), (df \to 8), (abc \to 8),$
- $(abd \to 7), (abf \to 7)$
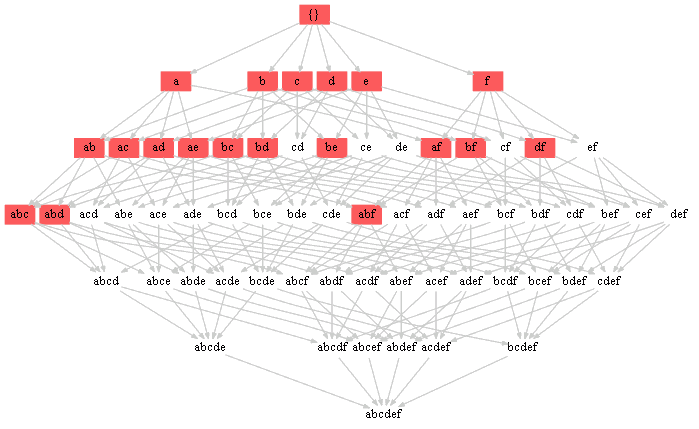
- note that here when we add an item the price always increases| | |
Properties
Properties of constraints in Lattice
Anti-Monotone
Anti-monotone constraint
- A constraint $q$ is ‘‘anti-monotone’’ iff
- when an itemset $X$ satisfies $q$, then any $Y \subseteq X$ also satisfies $q$.
- $q(X) \Rightarrow \forall Y \subseteq X : q(Y)$
Monotone
Monotone constraint
- A constraint $q$ is ‘‘monotone’’ iff
- when an itemset $X$ satisfies $q$, then any $Y \supseteq X$ also satisfies $q$.
- $q(X) \Rightarrow \forall Y \supseteq X : q(Y)$
Example
Example 1
- Frequency is a anti-monotonic constraint:
- $\text{freq}(X) \geqslant \gamma \Rightarrow \forall Y \supseteq X: \text{freq}(Y) > \gamma$
- sum of prices if a monotonic constraint:
- $\sum_{x \in X} x.\text{price} \leqslant \gamma \Rightarrow \forall Y \subseteq X: \sum_{y \in Y} y.\text{price} \leqslant \gamma$
Example 2
- $T_1 = {A,B,D,E}, T_2 = {A,B,C,D,F}, T_3 = {B,D,F}, T_4 = {C,E,F}$
- $p(A) = 2, p(B) = 4, p(C) = 1, p(D) = 3, p(E) = 4, p(F) = 4$
- Consider this constraint: $\sum_{x \in X} p(x) \leqslant 6$
- Assume that $X$ is an itemset. When we add something to $X$, the sum only can grow
- so this constraint is monotonic:
- $\forall X \subseteq Y, \sum_{y \in Y} p(y) \leqslant 6 \Rightarrow \sum_{x \in X} p(X) \leqslant 6$
- and if we remove an item, we’re sure that the price will decrease
Since it’s anti-monotone, can use Apriori to find all itemsets that satisfy it
- Level 1: $A, B, C, D, E, F$
- Level 2: $AB, AC, AD, AE, AF, BC, CD, CE, CF$
- Level 3: $ACD$
Summary
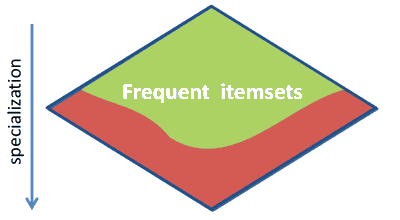
| Downward Closure | Upward Closure |
|---|---|
 |
 |
| - $freq(X, D) \geqslant t$ - $\min(X.\text{val}) \geqslant t$ - $\max(X.\text{val}) \leqslant t$ - $\text{sum}(X.\text{val}) \leqslant t$ - $X \subseteq \{A, B, C\}$ | - $freq(X, D) \leqslant t$ - $\min(X.\text{val}) \leqslant t$ - $\max(X.\text{val}) \geqslant t$ - $\text{sum}(X.\text{val}) \geqslant t$ - $X \supseteq \{A, B, C\}$ |
Convertible Constraints
Consider this dataset
- $T_1 = {A,B,D,E}, T_2 = {A,B,C,D,F}, T_3 = {B,D,F}, T_4 = {C,E,F}$
- $p(A) = 2, p(B) = 4, p(C) = 1, p(D) = 3, p(E) = 4, p(F) = 4$
And the following constraint
- $\text{avg}(X.\text{price}) \leqslant 3$
- it’s not anti-monotonic:
- $\text{avg}(B.\text{price}) = 4 \not \leqslant 3$, not satisfied
- $\text{avg}(AB.\text{price}) = 3 \leqslant 3$, satisfied
- it’s not monotonic either:
- $\text{avg}(A.\text{price}) = 2$ and $\text{avg}(AB.\text{price}) = 3$
but we can convert it into anti-monotone by ordering items by price acs:
- $C < A < D < B, E, F$
- now can traverse the search space in BFS-way - with Eclat
- need to enumerate items in lexicographical ordering for that:
- $C, CA, CAD, …$
Now we’re sure that the average always increases
- $\text{avg}(\varnothing) = 0, \text{avg}(C) = 1/1, \text{avg}(CA) = 4/2, \text{avg}(CAD) = 7/3, \text{avg}(CADF) = 11/4, \text{avg}(CADFE) = 16/5$
Papers
- Heikki Mannila, Hannu Toivonen: Levelwise Search and Borders of Theories in Knowledge Discovery. Data Min. Knowl. Discov. 1(3): 241-258 (1997) (about anti-monotone constraints)
- Jian Pei, Jiawei Han: Can we push more constraints into frequent pattern mining? KDD 2000: 350-354 (about convertible constraints)