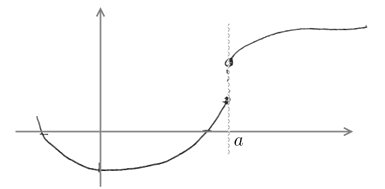
Continuous Functions
A Function $f(x)$ is continuous if the Limit of this function always exists otherwise the function is discontinuous
- $f(x)$ is continuous at $x = a$ if $\lim\limits_{x \to a} f(x) = f(a)$
- $f(x)$ is continuous everywhere if its continuous for all $a$ in the ‘'’domain’’’ of $f(x)$
Many functions are continuous, for example:
- Polynomial Functions
- Rational Functions
- Trigonometric Functions
- Exponential Functions and Logarithms
Careful| |- some functions might look discontinuous, but they may be continuous |- this is the case when the discontinuously-looking points are not in the domain
- but if the function is defined in this point, then it’s discontinuous
Discontinuous: