Function
In mathematics, a function $f(\cdot)$ is a set of pairs $x, f(x)$, where
- $x$ is input, $f(x)$ is output
- all possible inputs $x$ that a function can take is the ‘‘domain’’ of $f$
- all possible outputs $f(x)$ of a function $f(\cdot)$ is the ‘‘range’’ of $f$
<img src=””/>
Operations on Functions
Composition
For two functions $f$ and $g$, composition is $f \circ g$
- $(f \circ g) (x) = f(g(x))$
- $g$ is applied first, then $f$
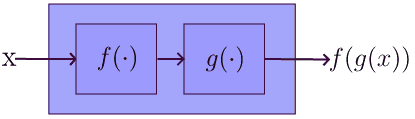
For example,
- $\sqrt{1 - x^2}$
- $g = x^2$, it’s inside
- $f(t) = \sqrt{1 - t}$, it’s outsize
Inverse
For $f$ its inverse is $f^{-1}$
- $x = f^{-1}(x)$ if $f(f^{-1}(x)) = x$
- $f^{-1}(\cdot)$ is a function that “undoes” $f(\cdot)$
Single Variable Functions
That’s the simplest type of functions: they have one input and one output
Important Function Classes
- Polynomial Functions: $P(x) = C_0 + C_1 x + \ … \ + C_n x^n = \sum_{k=0}^n C_k x^k$, $n$ is degree of $P(\cdot)$
- Rational Functions: $\cfrac{P(x)}{Q(x)}$, s.t. $Q(x) \ne 0$. e.g. $\cfrac{3x - 1}{x^2 - x - 6}$
- Trigonometric Functions: $\sin x$, $\cos x$, $\tan x$, etc
- Exponential Function and Logarithm
Continuous Functions
- Functions are continuous is their Limits always exist
- otherwise functions are discontinuous
- these are important functions in Calculus
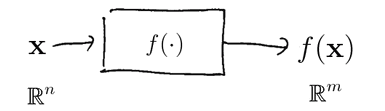
Multi Variable Functions
These functions are more complex:
- they can have multiple inputs and multiple outputs
Function Spaces
Functions, like Vectors, can form Vector Spaces
- they are called Function Spaces for functions