ML Wiki
Machine Learning Wiki - A collection of ML concepts, algorithms, and resources.

Dijkstra's Shortest Path

algorithms graphs

Dijkstra’s Shortest Path

Goal: to find the shortest path in a graph from a single-source s

input

  • directed graph $G = (V, E)$
  • each edge has non-negative length
  • source vertex $s$

output

  • for each $v \in V$ complete
  • $L(v)$ = length of the shortest path from $s$ to $v$ in $G$

Algorithm

Dijkstra’s(graph $G$, vertex $s$)

Initialization:

  • $X = {s}$: vertices we’ve processed so far
  • $A[s] = 0$: at the end, it’ll be populated with the shortest paths
  • $B[s] = \varnothing$ (empty path): computed shortest path, or explanation only

Main loop:

  • we examine all edges that came from $X$ to $V - X$
  • and among all vertices we pick one which gives the minimal score in Dijkstra’s greedy criterion $A[v] + l_{vw}$: we call it ‘‘minimizing edge’’

while $X \neq V$:

  • for all $(v, w) \in E$
  • with $v \in X$ and $w \notin X$
  • pick a pair that minimizes $A[v] + l_{vw}$ ($A[v]$ is already computed in earlier iterations)
  • let the minimizing edge be $(v^, w^)$
  • add $w^*$ to $X$
  • $A[w^] = A[v] + l_{v^w^}$: shortest path from $s$ to $w^$
  • $B[w^] = B[v^] + (v^, w^)$

Example

  • $s$ - starting vertex
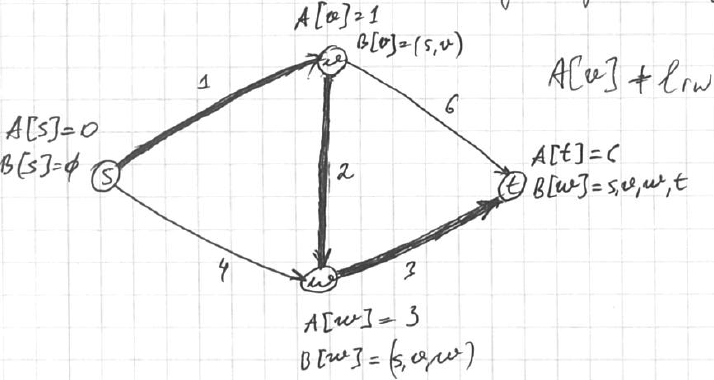  • <img src=”Image” >

Non-example

  • won’t compute the shortest path for non-negative edges   - <img src=”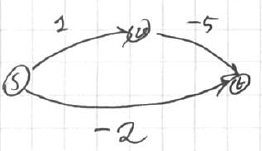Image” >

Implementation notes

  • don’t need the $B$ array
  • $\Theta(mn)$ - naive implementation of Dijkstra’s
  • with heaps - better speed

Heaps to speed up Dijkstra

invariants to keep with heaps

  • elements in heap: vertices in $V - X$ (not processed)
  • for $v \notin X$
    • $\text{key}[v]$ = smallest Dijkstra’s greedy score of $(u, v) \in E$ with $v \in X$
    • $\text{key}[v] = +\infty$ if an edge doesn’t exist

if maintain 2nd invariants

  • extract-min returns vertex $w^*$ to add to $X$ next

to maintain 2nd invariant

  • when we extract $w$ from heap (added to $X$)
  • for each edge $(w, v) \in E$
  • if $v \in V - X$ (i.e. already in the heap)
  • we update the key
    • delete $v$ from heap
    • recompute $\text{key}[x] = \min(\text{key}[u], A[w] + l_{wv})$
    • re-insert $v$ into heap

running time with heaps: $O(m \log_2 n)$

Implementation

```text only public static final int INFINITY = 1000000;

public static int[] dijkstra(UndirectedWeightedGraph graph, int s) { int dist[] = new int[graph.getN()]; Arrays.fill(dist, INFINITY);

List<HeapNode<Integer, Integer>> heapNodesList = prepareHeapNodesList(graph.getN());

Heap<Integer, Integer> heap = Heap.naturalMin();
HeapNode<Integer, Integer> sourceHeapNode = heap.insert(s, 0);
heapNodesList.set(s, sourceHeapNode);

for (int i = 0; i < graph.getN(); i++) {
    if (i |  = s) { |            HeapNode<Integer, Integer> result = heap.insert(i, INFINITY); |            heapNodesList.set(i, result);
    }
}

int n = graph.getN();

while (n > 0) {
    HeapNode<Integer, Integer> node = heap.extractFirst();
    int distance = node.getKey();
    int nodeNumber = node.getValue();
    dist[nodeNumber] = distance;

    for (Edge edge : graph.adjacent(nodeNumber)) {
        int to = edge.getTo();
        HeapNode<Integer, Integer> toNode = heapNodesList.get(to);
        int newDistance = distance + edge.getWeight();
        if (newDistance < toNode.getKey()) {
            heap.decreaseKey(toNode, newDistance);
        }
    }

    n--;
}

return dist; }

@SuppressWarnings(“unchecked”) private static List<HeapNode<Integer, Integer» prepareHeapNodesList(int n) { List<?> list = Arrays.asList(new HeapNode[n]); return (List<HeapNode<Integer, Integer») list; } ```

Heap implementation can be found here: Heap#Implementation

See also

Sources

✏️ Edit on GitHub