Graphs

Graphs

Consist of:

• vertices aka nodes ($V$)
• $n$ = number of vertices
• edges ($E$) = pair of vertices

• $m$ - number of edges

• can be ‘‘undirected’’ <img src=”” >
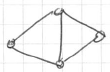• or ‘‘directed’’ <img src=”” >

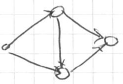Directed Acyclic Graph

This is a special kind of graph where

• there are no cycles
• and it is directed

These graphs can be sorted topologically

Representation

adjacency matrix

• $n \times n$ matrix where
• $A_{i,j} = 1$ if $G$ has $(i, j)$ edge
• or $+1$/$-1$ if directed
• or weight if weighted
• space required $\Theta(n^2)$

adjacency list

• array of vertices
• array of edges for each vertex
• space required $\Theta(n + m)$

Implementation

Adjacency list:

public class Graph {
    private int n;
    private final List<List<Integer>> adj;

    public Graph(int n) {
        this.n = n;
        this.adj = createAdjacentList(n);
    }

    private static List<List<Integer>> createAdjacentList(int n) {
        List<List<Integer>> res = new ArrayList<List<Integer>>(n);

        int i = 0;
        while (i < n) {
            res.add(new LinkedList<Integer>());
            i++;
        }

        return res;
    }

    public void addEdge(int v, int u) {
        adj.get(v).add(u);
    }

    public Iterable<Integer> adjacent(int v) {
        return adj.get(v);
    }

    public int getN() {
        return n;
    }
}

See also

• Minimal Cut Problem
• Graph Search (Breadth-First Search и Depth-First Search)
• Dijkstra’s Shortest Path
• Topological Ordering

Sources

• Algorithms Design and Analysis Part 1 (coursera)