ML Wiki
Machine Learning Wiki - A collection of ML concepts, algorithms, and resources.

Dot Product

geometry linear-algebra

Dot Product

Geometric Definition

Let $\vec v \cdot \vec w$ denote the ‘‘dot product’’ between vectors $\vec v$ and $\vec w$

  • definition: $\vec v \cdot \vec w = | \vec v | \cdot | \vec w | \cdot \cos \theta$ where $\theta$ is the angle between $\vec v$ and $\vec w$ - $| \vec v |$ denotes the length of $\vec v$ - if two vectors are perpendicular, then $\cos \theta = 0$ and thus $\vec v \cdot \vec w = 0$
  • if they co-directional, then $\theta = 0$ and $\vec v \cdot \vec w = | \vec v | \cdot | \vec w |$ |- consequently, we have $\vec v \cdot \vec v = | \vec v |^2$ | Image

Projections

Dot product is a projection:

  • let’s project $\vec v$ onto $\vec w$: $\text{proj}_{\vec w} (\vec v) = | \vec v | \cos \theta$ (by the $\cos$ definition) - we’re interested only in the direction of $\vec w$, so let’s normalize it to get $\hat w = \vec w / | \vec w |$ - it’s the unit vector in the direction $\vec w$ - $\vec v \cdot \hat w$ - dot product of $\vec v$ and some unit vector
    • $\vec v \cdot \hat w = | \hat w | | \vec v | \cos \theta = | \vec v | \cos \theta$ - it is a projection in the direction of $\vec w$
  • so $\vec v \cdot \hat w$ corresponds to the projection of $\vec v$ onto $\vec w$
  • $\text{proj}_{\vec w} (\vec v) = \vec v \cdot \hat w = | \vec v | \cos \theta$ - is the length of this projection - thus, $\vec v \cdot \vec w = | \vec v | | \vec w | \cos \theta = | \vec w | \cdot \text{proj}{\vec w} (\vec v) = | \vec v | \cdot \text{proj}{\vec v} (\vec w)$

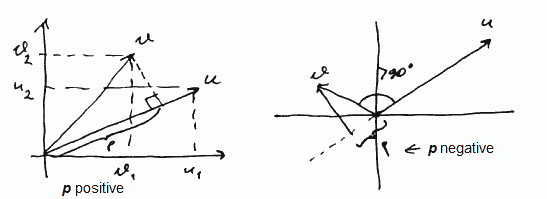
$p = \text{proj}_{\vec u} (\vec v) = \vec v \cdot \hat u = | \vec v | \cos \theta$ |- it can be positive or negative

  • positive when angle between vectors is less than $90^o$
  • negative when angle between vectors is greater than $90^o$

Image

The Cosine Theorem

Why does this geometric definition make sense?

  • consider vectors $\vec u$, $\vec v$ and $\vec w$
  • let $\vec v + \vec u = \vec w$ or $\vec u = \vec w - \vec v$
  • Image
  • $| \vec u |^2 = | \vec w - \vec v |^2 = (\vec w - \vec v) \cdot (\vec w - \vec v) = | \vec w |^2 + | \vec v |^2 - 2 \cdot \vec w \vec v$ - by the Cosine Theorem we know that
    • $| \vec u |^2 = | \vec w - \vec v |^2 = | \vec w |^2 + | \vec v |^2 - 2 \cdot | \vec w | \cdot | \vec v | \cdot \cos \theta$ - so $| \vec w | \cdot | \vec v | \cdot \cos \theta = \cfrac{1}{2} (| \vec w |^2 + | \vec v |^2 - | \vec w - \vec v |^2) = \cfrac{1}{2} (| \vec w |^2 + | \vec v |^2 - | \vec w |^2 - | \vec v |^2 + 2 \cdot \vec w \vec v) = \vec w \cdot \vec v$ - thus $\vec w \cdot \vec v = | \vec w | \cdot | \vec v | \cdot \cos \theta$ - i.e. the definition makes sense from the The Cosine Theorem point of view

Algebraic Definition

For two vectors $\mathbf v, \mathbf w \in \mathbb R^n$ we define the dot product as $\mathbf v^T \mathbf w = \sum\limits_{i = 1}^n v_i w_i$

Vector Orthogonality

$\mathbf v \; \bot \; \mathbf w \iff \mathbf v^T \mathbf w = 0$

Why?

  • by the Pythagoras theorem: $| \mathbf v |^2 + | \mathbf w |^2 = | \mathbf v + \mathbf w |^2$ - $\mathbf v^T \mathbf v + \mathbf w^T \mathbf w = (\mathbf v + \mathbf w)^T (\mathbf v + \mathbf w) = \mathbf v^T \mathbf v + \mathbf v^T \mathbf w + \mathbf w^T \mathbf v + \mathbf w^T \mathbf w$
  • or $\mathbf v^T \mathbf w + \mathbf w^T \mathbf v = 0$
  • note that $\mathbf v^T \mathbf w = \mathbf w^T \mathbf v$, so we have
  • $2 \mathbf v^T \mathbf w = 0$ or $\mathbf v^T \mathbf w = 0$

Equivalence of Definitions

Both definitions are equivalent.

I.e. $\vec v \cdot \vec w = \mathbf v^T \mathbf w = | \vec v | | \vec w | \cos \theta = \sum\limits_{i = 1}^n v_i w_i$ | Why?

  • let $\vec e_1, \ … \ , \vec e_n$ be the standard basis in $\mathbb R^n$
  • these vectors are orthonormal, i.e. $\vec e_i \cdot \vec e_j = \begin{cases} 1 & \text{if } i = j
    0 & \text{if } i \ne j
    \end{cases}$
  • let’s consider a dot product $\vec v \cdot \vec e_i$: $\vec v \cdot \vec e_i = | \vec v | \cos \theta = v_i$ - it’s a projection of $\vec v$ onto $ \vec e_i$ - which is $i$th component of $\vec v$ - we can project $\vec v$ and $\vec w$ onto the entire basis and get
  • $\vec v = \sum\limits_{i = 1}^n v_i \cdot \vec e_i$ and $\vec w = \sum\limits_{i = 1}^n w_i \cdot \vec e_i$
  • So, $\vec v \cdot \vec w = \vec v \cdot \sum\limits_{i = 1}^n w_i \vec e_i = \sum\limits_{i = 1}^n w_i (\vec v \cdot \vec e_i) = \sum\limits_{i = 1}^n v_i w_i$

$\square$

Sources

✏️ Edit on GitHub