Exponential Functions
- $e^x$, or $\exp x$ is the exponential function
- Logarithm is inverse of exponent
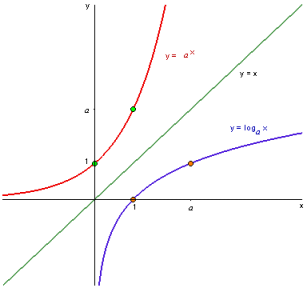
Base
- “Natural” base is $e = 2.718281828…$, where $e$ is the Euler’s Number
- can be any other base: $a^x$
Algebraic Properties
- $e^x e^y = e^{x + y}$
- $(e^x)^y = e^{xy}$
- $\cfrac{d}{dx} e^x = e^x$
- $\int e^x\, dx = e^x + C$
- relates Exponential Function and Trigonometric Functions
- $e^{ix} = \cos x + i \sin x$ where $i = \sqrt {-1}$
Taylor Expansion
Can expand $e^x = 1 + x + \cfrac{1}{2| }\, x^2 + \cfrac{1}{3!}\, x^3 + \cfrac{1}{4!}\, x^4 + \ … \ = \sum\limits_{k=0}^{\infty} \cfrac{1}{k!} x^k$ | |