Householder Transformation

Householder Transformation

Householder Transformation (also “Householder Reflection”) is an orthogonal reflection transformation:

• it reflex the vectors in the columns of the matrix such that
• the first vector has all zeros except the first element

The Transformation Matrix

Reflection transformation:

• Reflection across the plane orthogonal to some unit-vector $v$ is specified by the following transformation:
• $P = I - 2 v v^T$
• So this is just rank-1 update of the identity matrix
• such $P$ is called “Householder transformation” (also: Householder Reflection or Householder Matrix)
• and $v$ is the “Householder vector”
• when we multiply $P x$, $x$ is reflected around $\text{span}(v)^{\bot}$
• if $v$ is not unit vector, we need to normalize it

• let $\beta = 2 / | v |^2$, so we can simply write $P = I - \beta v v^T$

Properties

Householder matrices are symmetric and orthogonal: they are reflection matrices

Derivation

So we have $P = I - 2vv^T$:

• this is reflection across the plane orthogonal to $v$
• suppose we have some vector $x$ and want to reflect it such that it becomes parallel to some unit vector $y$
• 
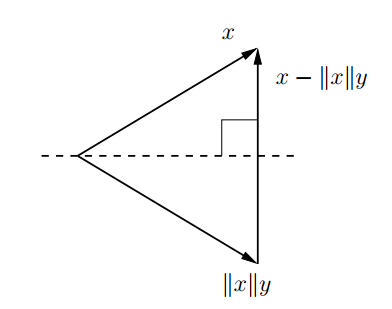
• here we want to reflect around the place that is between $y$ and $x$ - that bisects the angle between them

• the vector orthogonal to this place is $x - | x | y$

  - so let $u = x - | x | y$ and $v = u / | u |$

  - $| u |^2 = (x - | x | y)^T (x - | x | y) = \ …$

  - $… \ = | x|^2 - 2 | x | x^T y + | x |^2 | y |^2 = \ …$

  - $… \ = | x|^2 - 2 | x | x^T y + | x |^2 = \ …$ (since $y$ is unit vector)

  - $… \ = 2 | x|^2 - 2 | x | x^T y$

  - $Px = (I - 2 v v^T) x = x - 2 \cfrac{u u^T x}{| u |^2} = \ …$

  - $… \ = x - 2 \cfrac{(x - | x | y) (x - | x | y)^T x}{2 |x|^2 - 2 | x | x^T y} = \ …$

  - $… \ = x - 2 \cfrac{(x - | x | y) (x^T - | x | x^T y)}{2 |x|^2 - 2 | x | x^T y} = \ …$

  - $… \ = x - (x - | x | y) = | x | y$

  - so when we apply $P$ to some $x$, we get $| x | y$

We use such transformations for zeroing elements

• we want to zero all elements of $x$ except the first one, so we need $P x = \pm \alpha e_1$
• we know that if $P x = \pm \alpha e_1$ and $P$ is Householder reflection with $y = e_1$, then $P x =\pm \alpha e_1 = | x | e_1$, so $\alpha = \pm | x | = \rho | x |$ where $\rho = \pm 1$ |- let $z = x - \alpha e_1$ and $u = z / | z |$ |- so $z = x - \alpha e_1 = x - \rho | x | e_1 = \begin{bmatrix} |x_1
  x_2
  \vdots
  x_n \end{bmatrix} - \rho | x | \begin{bmatrix} |1
  0
  \vdots
  0
  \end{bmatrix} = \begin{bmatrix} x_1 - \rho | x | \ |x_2
  \vdots
  x_n \end{bmatrix} $
• we can choose any $\rho$, but often it’s $\rho = -\text{sign}(x_1)$ - this is better for round-off errors

QR Decomposition

Like in case of LU Decomposition, where we applied a series of Gauss Transformation changes, we can do the same and perform a series of Householder Transformations

• so if we select $y = \pm e_1$ (where $e_1$ is the matrix with 1 on position 1 and rest are zeros)
• then it will zero all elements of $x$ except the first one
• thus by the appropriate choice of $H$ we can take $A$ and zero all the sub-diagonal elements
• can do that multiple times for each column of $A$

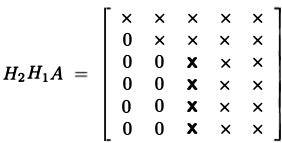
This way we can perform QR Decomposition:

def qr_householder(A): m, n = A.shape Q = np.eye(m) # Orthogonal transform so far R = A.copy() # Transformed matrix so far

 for j in range(n):
     # Find H = I - beta*u*u' to put zeros below R[j,j]
     x = R[j:, j]
     normx = np.linalg.norm(x)
     rho = -np.sign(x[0])
     u1 = x[0] - rho * normx
     u = x / u1
     u[0] = 1
     beta = -rho * u1 / normx
 
     R[j:, :] = R[j:, :] - beta * np.outer(u, u).dot(R[j:, :])
     Q[:, j:] = Q[:, j:] - beta * Q[:, j:].dot(np.outer(u, u))
     
 return Q, R

Hessenberg Decomposition

Instead of using it for reducting the matrix to Triangular, we can use Householder Transformation to reduce a matrix to Hessenberg Matrix

Sources

• http://www.cs.cornell.edu/~bindel/class/cs6210-f12/notes/lec16.pdf
• Matrix Computations (book)
• https://math.dartmouth.edu/~m116w17/Householder.pdf