Information Gain

machine-learning

Information Gain

The expected information gain is

the change in entropy when going
from a prior state
to anther new state

Entropy

Information

Consider two sequence of coin flips

HHTHTTH…
TTHHTTH…

How much information do we get after flipping each coin?

information: $I(X) = - \log_2 p(X)$
need a measure of unpredictability in a sequence of events
Expected Value of information -
- $\text{Entropy}(X) = E[I(X)] = \sum_x p(x) \cdot I(x) = - \sum_x p(x) \cdot \log_2 p(x)$

E.g.

coin: $P(H) = P(T) = 0.5$
- $I(X) = - \sum_i p(i) \log_2 p(i) = - (0.5 \log_2 0.5 + 0.5 \log_2 0.5) = 1$
dice: $p(i) = 1/6$
- $I(X) = - \sum_i p(i) \log_2 p(i) = - 6 \cdot (\frac{1}{6} \log_2 \frac{1}{6}) \approx 2.58$
- more unpredictable than a coin
weighted dice: $p(1) = … = p(5) = 0.1$ and $p(6) = 0.5$
- $I(X) = - 5 \cdot (0.1 \log_2 0.1) - 0.5 \log_2 0.5 \approx 2.16$
- less unpredictable than a fair dice

Entropy Function

Given $m$ classes, the entropy of signal $S$ is

$I(S) = - \sum_{i=1}^{m} p_i \log_2 (p_i)$
where $p_i$ is probability of seeing class $C_i$ in $S$
$S_i$ - set of all records of class $i$

Split in Halves

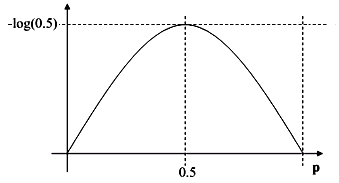
Entropy for Two Classes

For two classes:

If records in $S$ belong to classes $C_1$ or $C_2$

Let $p_1 = (

S_1

) = p$ and $p_2 = (

S_2

) = 1 - p$

- Then, $E[I(S)] = -p \cdot \log_2 (p) - (1 - p) \cdot \log_2 (1-p) $

expected value of entropy with two subsets

Entropy is maximal when $p_1 = p_2 = 0.5$

when $p_1 = 0$ and $p_2 = 1$ (or vise versa), there’s no entropy

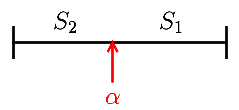
Splitting

Suppose we want to split a set $S$ into two parts $S_1$ and $S_2$

we compute the entropy before splitting
and compute the entropy after splitting at some point $\alpha$
the ‘‘information gain’’ of splitting is the entropy before minus the expected entropy after

$I(S, \alpha) = I(S) - E[I({S_1, S_2})] = I(S) - p_1 \cdot I(S_1) - p_2 \cdot I(S_2)$

where $p_1 = \cfrac- and $S_1, S_2$ are subsets of $S$ s.t. $S_1 \equiv { s \ : \ s < \alpha }$ and $S_2 = S - S_1$
note that I(S) is a constant and doesn’t depend on $\alpha$

Best Splitting

What is the best $\alpha$:

we want to select a boundary $\alpha$ that maximizes the information gain

So for all possible values of $\alpha$

we compute the information gain
and select the best splitting
the process can be repeated recursively

Example 1

Can give the answer of “how much unpredictable is your data?”

suppose that for the titanic dataset ([http://www.kaggle.com/c/titanic-gettingStarted/data]) we have 342 survived people out of 891
$p(\text{Survive}) = \cfrac{342}{891}$
\text{Entropy} = - \cfrac{342}{891} \log_2 \cfrac{342}{891} - \cfrac{549}{891} \log_2 \cfrac{549}{891} \approx 0.96

This is important measure for splitting in Decision Trees

select the attribute with the highest information gain
it will reduce the unpredictability the most

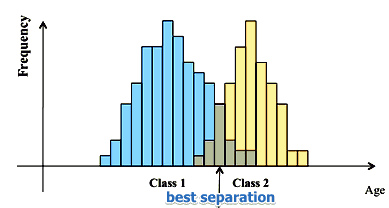
Example 2

Suppose we have a data set of customers

class $C_1$ - drinks milk and $C_2$ - doesn’t drink
what’s the best boundary to split the age variable?

Sources

✏️ Edit on GitHub

Information Gain