Inversion Count
Sequence inversion
- In a sequence $\pi = \langle a_0, …, a_t \rangle$ or elements $A = { a_i }$
- a pair $(a_i, a_j)$ is an ‘‘inversion’’ if $i < j \land a_i > a_j$
- the number of such inversions is the inversion number of sequence $\pi$
- this is a measure of “sortedness” of sequence $\pi$
Two ranked vectors
- An inversion in two rankings $r_1, r_2$ of the same variable $X$ is
-
a pair $(x_i, x_j) \ \ r_1(x_i) < r_1(x_j) \land r_2(x_i) > r_2(x_j)$ - it’s called a ‘‘pair-wise disagreement’’ between two ranking lists
Graphical Counting
we can represent two rankings as a Bipartite Graph $G = \langle N, S, E \rangle$
- $N = r_1(X)$ and $E = r_2(X)$ being two disjoint set of nodes
- $X$ is some variable, and $r_1$ and $r_2$ are different rankings of this variable
- $E$ is set of edges $E = \Big{ \big(r_1(x), r_2(x) \big) \Big} $ i.e. corresponding elements of $X$ are connected in this graph
Counting:
- '’bilayer drawing’’ of $G$ is when there are two parallel lines, edges of $N$ are drawn on one, and edges of $S$ are drawn on another
- '’bilayer cross count’’ is a pairwise intersections edges of $N$ and $S$
- bilayer cross count corresponds to the number of inversions when $N$ and $S$ are ranking vectors
Example:
- $X = { A, B, C, D, E }$
- two ranking $r_1 = \langle E, B, A, C, D \rangle$ and $r_2 = \langle B, E, C, D, A \rangle$
- draw this is a bipartite graph and count the number of intersections
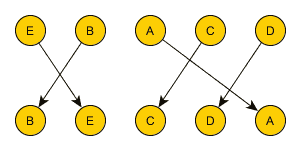
- so there are 3 inversions in these two rankings
Algorithms
A modification of Merge Sort can compute the # of inversions in $O(| N| \log |N|)$ |- see Merge Sort#Counting Inversions
See Also
Sources
- Simple and efficient bilayer cross counting [http://www.emis.de/journals/JGAA/accepted/2004/BarthMutzelJuenger2004.8.2.pdf]
- http://en.wikipedia.org/wiki/Inversion_(discrete_mathematics)
- Algorithms Design and Analysis Part 1 (coursera)