Merge Sort

Merge Sort

Sorting algorithm based on Divide and Conquer computational paradigm

Algorithm

MergeSort(array $a$):

• split $a$ into 2 halves
• sort them recursively
• merge the result

Implementation

Java

```tera term macro public int[] mergeSort(int[] input) { int n = input.length; if (n <= 1) { return input; }

int middle = n / 2;
int leftUnsorted[] = Arrays.copyOfRange(input, 0, middle);
int rightUnsorted[] = Arrays.copyOfRange(input, middle, n);

int left[] = mergeSort(leftUnsorted);
int right[] = mergeSort(rightUnsorted);

return merge(left, right); }

public int[] merge(int[] left, int[] right) { int leftLen = left.length, rightLen = right.length; int res[] = new int[leftLen + rightLen];

int leftIndex = 0, rightIndex = 0, resIndex = 0;

while (leftIndex < leftLen && rightIndex < rightLen) {
    if (left[leftIndex] <= right[rightIndex]) {
        res[resIndex] = left[leftIndex];
        leftIndex++;
        resIndex++;
    } else {
        res[resIndex] = right[rightIndex];
        rightIndex++;
        resIndex++;
    }
}

while (leftIndex < leftLen) {
    res[resIndex] = left[leftIndex];
    leftIndex++;
    resIndex++;
}

while (rightIndex < rightLen) {
    res[resIndex] = right[rightIndex];
    rightIndex++;
    resIndex++;
}

return res; } ```

Scala

def msort(xs: List[Int]): List[Int] = {
  val n = xs.length / 2
  if (n == 0) {
    xs
  } else {
    val (fst, snd) = xs splitAt n
    merge(msort(fst), msort(snd))
  }
}
 
def merge(xs: List[Int], ys: List[Int]) = xs match {
  case Nil => ys 
  case x :: xs1 =>
    ys match {
      case Nil => xs
      case y :: ys1 =>
        if (x < y) x :: merge(xs1, ys)
        else y :: merge(xs, ys1)
    }
}

Applications

Counting Inversions

With little modification the merge sort algorithm can be turned in the counting inversions algorithm.

Goal

• Input: array $A$ containing $1..n$ in some arbitrary order
• Output: number of inversions
  • i.e. number of pairs $(i, j)$ of array indices with $i < j$ and $A[i] > A[j]$

Motivation

• how close are the two ranked lists?
• i.e. of 2 friends with movies

Example

• 1 3 5 2 4 6
• <img src=”” >
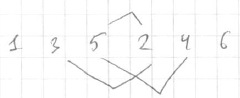• if we write the sorted input and the given input, number of crosses would be number of inversions
• <img src=”” >
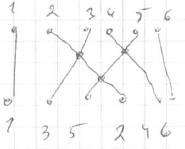• inversions are $(3,2)$, $(5,2)$, $(5,4)$

Brute force is not an option: $\Theta(n^2)$ time

Basic idea:

• insertion $c(i, j)$ is
  • ’'’left’’’, if $i, j \leqslant \frac{n}{2}$
  • ’'’right’’’, if $i, j > \frac{n}{2}$
  • ’'’split’’’ if $i \leqslant \frac{n}{2} < j$

Algorithm

count(array $A$, length $n$): [idea]

• if $n$ = 1 return 0
• $X$ = count(1st half of $A$, $n / 2$)
• $Y$ = count(2nd part of $A$, $n / 2$)
• $Z$ = count-split($A$, $n$)
• return $X + Y + Z$

Count split should be linear to get $O(n \log n)$ running time. So we may modify merge sort and get:

count-and-sort(array $A$, length $n$):

• // B - sorted version of 1st half, C - of 2nd, D - (A, B) merged
• if $n$ = 1 return 0
• $(B, X)$ = count-and-sort(1st half of $A$, $n/2$)
• $(C, Y)$ = count-and-sort(2nd half of $A$, $n/2$)
• $(D, Z)$ = count-split($A$, $n$)
• return $(D, X + Y + Z)$

merge-count-split:

• while merging the two sorted subarrays, count the number of split inversions
• when element of 2nd array C is copied to output D
  • increment total by number of elements remaining in 1st array B

Example

• consider merging (1, 2, 3) {L} with (2, 4, 6) {R}
• when 2 is copied to the output, it discovers the split inversions (3, 2) and (5, 2)
• when 4 is copied, it finds (5, 4)
• when in R element is less than in L - that’s an inversion| | |

  Implementation

  ```tera term macro public Pair<int[], Long> countAndSort(int[] input) { int n = input.length; if (n == 1) { return Pair.of(input, 0L); }

  int middle = n / 2; int leftUnsorted[] = Arrays.copyOfRange(input, 0, middle); int rightUnsorted[] = Arrays.copyOfRange(input, middle, n);

  Pair<int[], Long> left = countAndSort(leftUnsorted); Pair<int[], Long> right = countAndSort(rightUnsorted); Pair<int[], Long> split = countSplitAndMerge(left.getLeft(), right.getLeft());

  return Pair.of(split.getLeft(), left.getRight() + right.getRight() + split.getRight()); }

public Pair<int[], Long> countSplitAndMerge(int[] left, int[] right) { int leftLen = left.length, rightLen = right.length; int sortedOutput[] = new int[leftLen + rightLen];

int leftIndex = 0, rightIndex = 0, resIndex = 0;

long inversions = 0;

while (leftIndex < leftLen && rightIndex < rightLen) {
    if (left[leftIndex] <= right[rightIndex]) {
        sortedOutput[resIndex] = left[leftIndex];
        leftIndex++;
        resIndex++;
        // nothing
    } else {
        sortedOutput[resIndex] = right[rightIndex];
        rightIndex++;
        resIndex++;

        int remainedInLeft = leftLen - leftIndex;
        inversions = inversions + remainedInLeft;
    }
}

while (leftIndex < leftLen) {
    sortedOutput[resIndex] = left[leftIndex];
    leftIndex++;
    resIndex++;
}

while (rightIndex < rightLen) {
    sortedOutput[resIndex] = right[rightIndex];
    rightIndex++;
    resIndex++;
}

return Pair.of(sortedOutput, inversions); }

@Override public void run() { int[] input = readInput(); Pair<int[], Long> result = countAndSort(input); out.print(result.getRight()); } ```

External Merge Sort

The merge sort algorith is very easy to extend to sort large amounts of data that don’t fit into memory - see External Merge Sort

See Also

• Divide and Conquer
• Quick Sort

Sources

• Algorithms Design and Analysis Part 1 (coursera)