Iterative Removal
This is an application of the Dominance principle in the Game Theory.
A game is called ‘‘dominance solvable’’ if it can be solved with Iterative Removal
Iterated elimination or Iterative removal algorithm:
- for a game $G$ with set of strategies $A$
- find a dominated strategy $a$
- let $A \leftarrow A - { a }$ i.e. remove this strategy from the game
- repeat till there are no dominated strategies
Properties
Note:
- removal of strictly dominated strategies is always good
- it preserves the Nash Equilibrium of the game
- however for weekly dominated strategies you should be more careful
- order of removal may matter
Property 1
If a matrix game (Normal Form Game) can be solved by using iterative removal of strictly dominated strategies
- (1) then the found solution is a Nash Equilibrium
- (2) this equilibrium is unique
Recall that a profile $(s^_1, s^_2)$ is a Nash Equilibrium if
- $u_1(s^_1, s^_2) \geqslant u_1(s_1, s^*_2), \forall s_1 \in S_1$
- $u_2(s^_1, s^_2) \geqslant u_2(s^*_1, s_2), \forall s_2 \in S_2$
- (i.e. we just fix one solution and see if somebody wants to deviate)
; Part 1: the found profile is a Nash Equilibrium
- (by contraction)
- suppose $(s^_1, s^_2)$ is not a Nash Equilibrium
- i.e. we assume the opposite of the definition (negate it)
- $\exists s_1 \in S_1: u_1(s_1, s^_2) > u_1(s^_1, s^*_2)$ and
- $\exists s_2 \in S_2: u_1(s^_1, s_2) > u_1(s^_1, s^*_2)$
- since we ended up with $(s^_1, s^_2)$, the profile $(s_1, s_2)$ was removed during the iterative removal
- it happened because either
- (1) $p_1$ removed $s_1$ (the row was eliminated) or
- (2) $p_2$ removed $s_2$ (the column was eliminated)
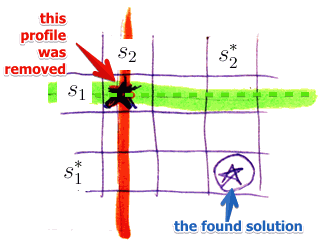
- (1) suppose $p_1$ removed $s_1$
- he removed the whole row along with the profile $(s_1, s^*_2)$
- $\Rightarrow (s_1, s^_2)$ was dominated by some other strategy profile, say $(s’_1, s^_2)$
- but since we ended up with $(s^_1, s^_2)$ then
- either $s’_1 = s^*_1$ or
- $u(s^_1, s^_2) > (s’_1, s^_2)$ and $(s’_1, s^_2)$ was also removed
- but we assumed that $u_1(s_1, s^_2) > u_1(s^_1, s^*_2)$
- $\Rightarrow$ contradiction
- (2) is shown analogously to (1)
; Part 2: the equilibrium is unique
- (by contradiction)
- assume it’s not unique
- i.e. there $\exists$ another NE $(\tilde{s}_1, \tilde{s}_2)$ which was removed during the iterative removal
- again two cases: $(\tilde{s}_1, \tilde{s}_2)$ was removed in (1) a row by $p_1$, (2) in a column by $p_2$
- case 1: it was removed by $p_1$ in a row
- i.e. there was some other alternative that was better:
- $\exists s_1 \in S_1: u_1(s_1, \tilde{s}_2) > u_1(\tilde{s}_1, \tilde{s}_2)$
- but it contradicts the definition of a Nash Equilibrium
- case 2: it was removed by $p_2$ in a column
- $\exists s_2 \in S_2: u_2(\tilde{s}_1, s_2) > u_2(\tilde{s}_1, \tilde{s}_2)$
- this again contradicts the definition
$\square$
This means we never can remove a NE by iterative removal.
Examples
Example 1
Consider this Normal Form Game with 2 players and with 3 actions each
| $p_2 \to$ $p_1 \downarrow$ |
$L$ | $C$ | $R$ | $T$ | (1,0) | (1,3) | (3,0) | $M$ | (0,2) | (0,1) | (3,0) | $B$ | (0,2) | (2,4) | (5,3) |
First we eliminate strategy $R$ for player $p_2$
- it’s dominated by $C$
| $p_2 \to$ $p_1 \downarrow$ |
$L$ | $C$ | $R$ | $T$ | (1,0) | (1,3) | (3,0) | $M$ | (0,2) | (0,1) | (3,0) | $B$ | (0,2) | (2,4) | (5,3) |
Then we can remove $M$ for $p_1$
- it’s dominated by $B$
| $p_2 \to$
$p_1 \downarrow$ | $L$ | $C$ | $R$ | $T$ | (1,0) | (1,3) | (3,0) || $M$ | (0,2) | (0,1) | (3,0) || $B$ | (0,2) | (2,4) | (5,3) |
Next, remove $L$ - it’s dominated by $C$
| $p_2 \to$
$p_1 \downarrow$ | $L$ | $C$ | $R$ | $T$ | (1,0) | (1,3) | (3,0) || $M$ | (0,2) | (0,1) | (3,0) || $B$ | (0,2) | (2,4) | (5,3) |
And finally remove $T$
| $p_2 \to$
$p_1 \downarrow$ | $L$ | $C$ | $R$ | $T$ | (1,0) | (1,3) | (3,0) || $M$ | (0,2) | (0,1) | (3,0) || $B$ | (0,2) | (2,4) | (5,3) |
The action profile $(B, C)$ is the solution
Example 2
Consider the following matrix game:
| | $C_1$ | $C_2$ | $C_3$ | $R_1$ | (1, 3) | (2, 4) | (1, 0) || $R_2$ | (3, 3) | (5, 2) | (0, 1) || $R_3$ | (2, 5) | (2, 0) | (1, 8) | Remove strategies iteratively:
- $R_3 \ D \ R_2$ (where $D$ is the dominance relation)
- $C_2 \ D \ C_1$
- no other elimination can be made
| | $C_1$ | $C_2$ | $C_3$ | $R_1$ | (1, 3) | (2, 4) | (1, 0) || $R_2$ | (3, 3) | (5, 2) | (0, 1) || $R_3$ | (2, 5) | (2, 0) | (1, 8) | So we end with the following matrix:
| | $C_1$ | $C_3$ | $R_2$ | (3, 3) | (0, 1) || $R_3$ | (2, 5) | (1, 8) | Now apply the Nash Equilibrium rule
- $(R_3, C_1)$ - not an equilibrium, both players want to deviate
- same for $(R_2, C_3)$
- the Nash Equilibria are $(R_2, C_1)$ and $(R_3, C_3)$ - they are stable and no one wants to deviate