Unanimity
Unanimity is principle from Voting Theory that is the same as Dominance:
If a candidate $a$ is always preferred by the majority to $b$, then we can say that $b$ is dominated by $a$ and never consider $b$ again
Pareto-Optimal Solutions
In Multi-Objective Optimization and Multi-Criteria Decision Aid there could be many “best” solutions - these solutions are called the Pareto-Optimal solutions
Consider this example:
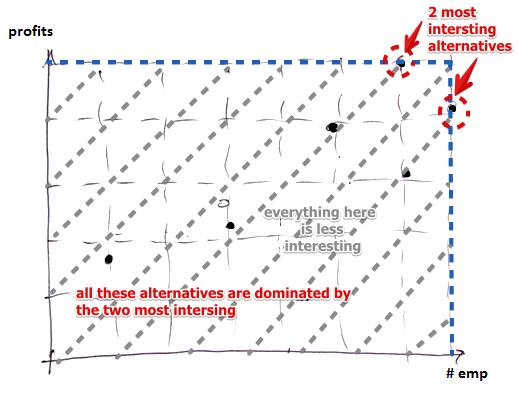
- the two alternatives along the blue line form the pareto-optimal set
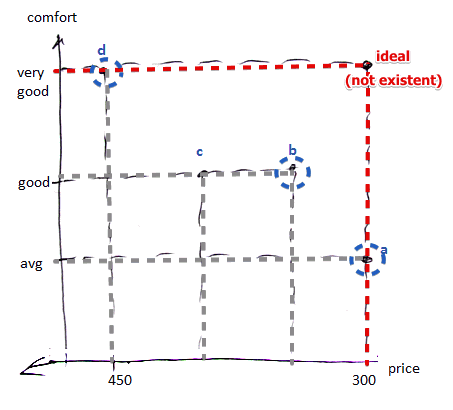
- the solutions in blue circles also form the pareto-optimal set
Dominance
- for the second examples we can say that $b$ ‘‘dominates’’ $c$:
- $b$ has the same level of quality, but it is cheaper
- we can remove all ‘‘dominated’’ solutions from the solution space and this will give us the Pareto-optimal set of solutions
- in MOO this is also called the set of efficient solutions
- ; dominance
- $a$ dominates $b$ $\iff \forall i: f_i(a) \geqslant f_i(b)$ and $\exists i: f_j(a) > f_j(b)$
- i.e. for all criteria $a$ is at least as good as $b$, but there’s at least one criteria at which $a$ is strictly better than $b$
This is not always good. Consider this example
- you’re looking for an apartment to rent
- you consider price and distance to work (want to minimize both)
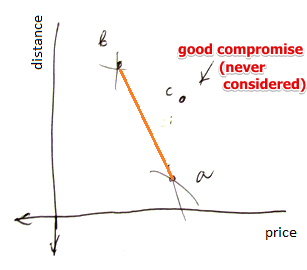
- in this case $c$ is dominated by $a$ and $b$:
- $b$ is very cheap, $a$ is very close
- $c$ is a good compromise, but it’s dominated
Another example
- suppose we’re choosing a car
- there are 4 criteria: price, power, consumption, comfort
- there are 6 alternatives
| | Price | Power | Consumption | Comfort | Avg A. | 18 | 75 | 8 | 3 || Sport | 18.5 | 110 | 9 | 2 || Avg B. | 17.5 | 85 | 7 | 3 || Lux 1 | 24 | 90 | 8.5 | 5 || Exonomic | 12.5 | 50 | 7.5 | 1 || Lux 2 | 22.5 | 85 | 9 | 4 | We see that ‘'’Avg B’’’ is always better than ‘'’Avg. A’’’
- then nobody will ever choose Avg A: A is dominated by B
No other alternative can be eliminated this way
Game Theory
This principle is as well applied in the Game Theory
Notation:
- $A_i$ - set of strategies for player $i$
- $u_i$ - the utility function of $i$
- $a, b \in A_i$ - two strategies in $A_i$
- denote $A_{-i}$ as the set of all strategies for other players
- ; Strict dominance
- $a$ ‘’ ‘'’strictly’’’ dominates’’ $b$ if $\forall c \in A_{-1}: u_i(a, c) > u_i(b, c)$
- in other words: $a$ strictly dominates $b$ is for every action that other players can take, the action $a$ gives $i$ better payoff than $b$
- ; Weak dominance
- $a$ ‘‘(weakly) dominates’’ $b$ if $\forall c \in A_{-1}: u_i(a, c) \geqslant u_i(b, c)$
If $a$ dominates all other strategies $b$ of the player $i$ then it’s ‘‘dominant’’
- in a strategy profile if every player plays their dominant strategies then it’s a Nash Equilibria
- this idea is used in Iterative Removal for solving Normal Form Games
Pareto Optimality
In Game Theory there’s also a notion of Pareto Optimality
Suppose you see a game as an outside observer, not a player
- Can we say that one outcome $O$ is better than some other outcome $O’$?
Pareto-Dominance
- suppose there’s one outcome $O$ that is as good as some other outcome $O’$ for all players
- but there’s one agent $i$ who strictly prefers $O$ to $O’$
- then $O$ is considered better than $O’$
- and $O$ ‘‘pareto-dominates’’ $O’$
Pareto-Optimality
- outcome $O^*$ is ‘‘pareto-optimal’’ if there is no other outcome that pareto-dominates it
- a game can have more than one pareto-optimal outcome
- for Zero-Sum Games every outcome is pareto-optimal
Problems
Close Contenders
$b$ is a close contender if
- it’s dominated by some alternative $a$
- but $b$ is still a good choice
Consider this example:
- $A = {a, b, c, d}$
- $A^* = {a, c, d}$ - efficient (pareto-optimal) set of solutions
| $c$ | $e_1$ | $e_2$ | $e_3$ | $…$ | $e_{100}$ | $a$ | 100 | 100 | 100 | … | 100 || $b$ | 99 | 99 | 99 | … | 99 || $c$ | 101 | 0 | 0 | … | 0 || $d$ | 0 | 101 | 0 | … | 0 | But we see that $c$ and $d$ aren’t that good, but both are in $A^*$
- i.e. we should have taken $b$ instead them