K-Means LSH

K-Means LSH

Many of LSH families are structured quantizers: they don’t take into account underlying statistics

• for example, E2LSH is structured:
• we choose only quantization step $w$ and offset $b$ and have little influence on the density of individual cells
• but can address this issue by learning a Vector Quantizer - such as K-Means: this way we can adapt the cell size to the density of the space in the cell

Learning Density with K-Means

Unstructured VQ:

• let $\mathcal R \to [ \, 1, 2, \ … \ , k \, ]$
• and $\mathbf x \to g(\mathbf x) = \mathop{arg min}\limits_{i = 1..k} L_2(\mathbf x, \boldsymbol \mu_i)$
• it maps each vector to a cell indexed by $g(\mathbf x)$
• $k$ is # of possible values of $g(\cdot)$
• $\boldsymbol \mu_i$ are centroids - they define the quantizer
• often learned with K-Means

Illustration:

• 
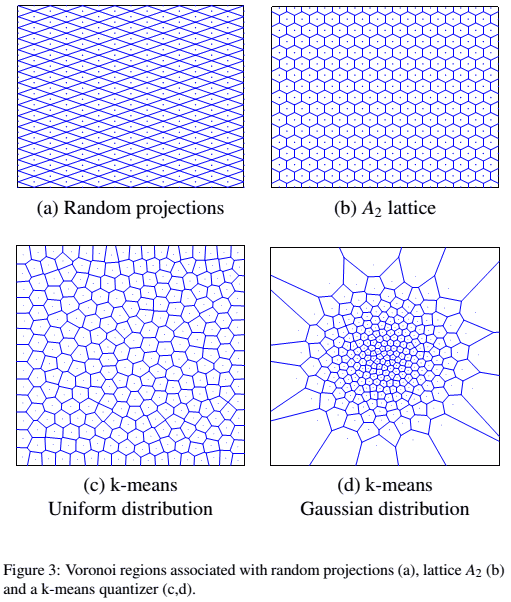
• Euclidean LSH (Random Projection LSH) vs K-Means
• K-Means adapts to data while others don’t
• source: Paulevé2010 figure 3

KLSH: K-Means LSH

Preprocessing

How to use K-Means to build a LSH?

• generate $L$ different clusterings on the same data by using different seeds
• after this we have $L$ codebooks (sets of centroids) ${\mathbf c_{j1}, \ … \ , \mathbf c_{jk}}$, where $\mathbf c_{ji}$ is $i$th centroid of $j$’s clustering
• each centroid is an $h$ and codebooks is an $g$ in LSH

Indexing:

• a vector to index is assigned to the closest centroid found in a codebook
• use $L$ codebooks to have $L$ cluster assignments

Querying

Search time:

• first nearest centroid for each codebook
• then keep only vectors that are assignment to the same centroids

query($\mathbf q$)

• $\text{res} = \varnothing$
• for $j = 1$ to $L$ do

  • $i^* = \operatorname{arg\, mix}\limits_{i = 1 .. k} | \mathbf q, \mathbf c_{ji} |$

    - $\text{res} = \text{res} \cup \big{ \text{cluster}(\mathbf c_{ji^*}) \big}$

• return $\text{res}$

Improvements

Multi-Probing

Multi-Probing for K-Means LSH:

• fix $m_p$ the number of buckets we want to retrieve
• for each $L$ hash functions
  • select $m_p$ closets centroids
  • then return all vectors from these $m_p$ centroids

Query-Adaptive K-Means LSH

Idea:

• a variation of Query-Adaptive LSH for K-Means LSH
• instead of a single k-means per hash maintain a pool of independent clustering results
• at the query time select the best one from the pool

Usual Query-Adaptive LSH:

• define a pool of $L$ hash functions (with $L$ larger than in usual LSHs)
• compute relevance criteria $\lambda_j$ for each $g_j$: this criteria identifies the hash functions that are more likely to return the NNs
• relevance could be: distance between the query and the center of the cell

Query-Adaptive K-Means LSH:

• $\lambda_j(\mathbf q) = \min_{i = 1..k} | \mathbf q, \mathbf c_{ji} |$

  - and $\lambda_j(\mathbf q)$ is actually a by-product of finding the nearest centroid

• so rank $g_j(\mathbf q)$ by $\lambda_j(\mathbf q)$ then pick $p$ best and use them

Notes:

• for this to be useful need $L$ larger than usual
• it gives better performance, but it becomes more computationally expensive - may be not very critical as it’s done offline

Speeding K-Means Up

Can use Approximate K-Means or Mini-Batch K-Means

Sources

• Paulevé, Loïc, et al. “Locality sensitive hashing: A comparison of hash function types and querying mechanisms.” 2010. [https://hal.inria.fr/inria-00567191/document]