Locality Sensitive Hashing
In large databases it’s not possible to use brute force search: there’s too much data
- one way of speeding search up is using Indexing: in particular, most interesting indexes are Multi-Dimensional Indexes
- but many of these “classical” indexing schemes don’t work for high dimensional data
- ’'’Locality-Sensitive Hashing’’’ algorithms address this problem:
- it’s a family of probabilistic/approximate indexing techniques that return the true KNNs most of the time correctly
LSH algorithms:
- used for quick search of similar entires in larges DBs
- used for Nearest Neighbor (1-NN) queries as well as in KNN queries
-
these algorithms are ‘‘randomized’’: they don’t guarantee the exact answer, but rather give a high probability to find the correct answer or a close approximation
- Good similarity/distance function should rank relevant answers much closer to the query than irrelevant
- if it’s the case, approximate answer should also give good result
- Outcome: by allowing some small error and storage overhead, can considerably improve the query time
Basic idea
- hash points s.t. probability of collision is high for similar objects
Applications
- Finding duplicates and near-duplicates
- Audio, video, image search
- Pattern Classification
- Cluster Analysis
Problem Definition
Nearest Neighbor Search Problem
Notation:
-
$| \mathbf x |_p = \left( \sum_i x_i ^p \right)^{1/p}$ - let $d_p(\mathbf p, \mathbf q) = | \mathbf p - \mathbf q |_p$ - and let $d_H(\mathbf p, \mathbf q)$ be the Hamming Distance: # of bits in which $\mathbf p$ and $\mathbf q$ are different
NN Search problem:
- Given set $P$ of $n$ objects preprocess $P$ s.t. it’s effective to find $\mathbf p \in P$ closest to a query object $\mathbf q$
- KNN: return top $k$ closest objects ${ \mathbf p_1 , \ … \ , \mathbf p_k }, \mathbf p_i \in P$
$\varepsilon$-NNS problem:
- approximate version of NNS
- $\mathbf p \in P$ closest to a query object $\mathbf q$ s.t. $d(\mathbf p, \mathbf q) \leqslant (1 + \varepsilon) \cdot d(\mathbf p^, \mathbf q)$ where $\mathbf p^$ is the true NN
- can generalize to KNN as well:
- find $\mathbf p_1 , \ … \ , \mathbf p_k \in P$ s.t. distance $d(\mathbf p_i, \mathbf q)$ is at most $(1 + \varepsilon)$ to the true $i$th closest $\mathbf p^*_i$
Most Similar Item Problem
- Given a query point $q$ and a database $D$
- find $q’ \in D$ s.t. $q’$ is the most similar object to $q$
Brute force solution:
- try each object in the database and return the closest
-
the complexity of executing this query grows linearly with $N = D $: number of items in the database
Trees
- e.g. kd-Trees, Quad Trees, R-Trees
- the complexity is $O(\log N)$
- problem: when dimensionality is big, they break down, and we end up testing all the nodes - which brings the complexity back to $O(N)$
- A hash table is a structure that allows to map between some symbol and some value
- a well-designed hash function should separate two close symbols into different buckets of a hash table
- so hashes are good for exact matches, but we need to get NN match
Cryptographic hashes like MD5 or SHA1:
- change one bit - get a completely different hash
- but we want to same same hash for close objects
- Solution: Use LSH
LSH Problem
- given $q$ find closest $q’ \in D$
- with probability $(1 - \delta)$ we return the true NN
Basic idea:
- use LSH: a special hash function that would put points that are close together to the same point
- if two points are close together in high-dimensional space, then they should remain close together after some projection to a lower-dimensional space
Illustration:
- suppose we have a 3D sphere with points on it
- if we project the sphere on 2D, then close points should still remain close - no matter how we rotate the sphere
- if points are far apart, usually in the projection they are also far apart, but sometimes they become close
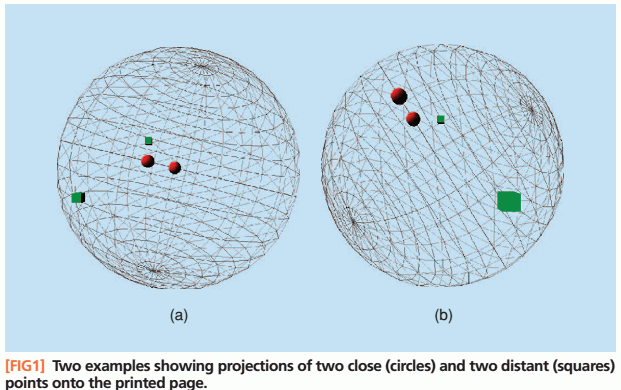
- (Source: fig1 of Slaney2008)
Formalization:
- let $D(\cdot, \cdot)$ be a distance function of elements from $P$
- then for each $\mathbf p \in P$ let $B(\mathbf p, r)$ be a set of elements within distance $r$ from $\mathbf p$
A family of hash functions $\mathcal H$ is $(r_1, r_2, p_1, p_2)$-sensitive if
- for all $\mathbf p, \mathbf q$
- if $\mathbf p \in B(\mathbf q, r_1)$ then $P_{\mathcal H} \Big[ h(\mathbf q) = h(\mathbf p) \Big] \geqslant p_1$
- if $\mathbf p \not \in B(\mathbf q, r_2)$ then $P_{\mathcal H} \Big[ h(\mathbf q) = h(\mathbf p) \Big] \leqslant p_2$
LSH:
- A LSH family is useful when $p_1 > p_2$ and $r_1 < r_2$
- The algorithin solves $(r, \varepsilon)$-NN problem if
- if there exists a $\mathbf p^* \in B(\mathbf q, r_1)$ then $g_j(\mathbf p^*) = g_j(\mathbf q)$ for at least one $j$
Common for almost all LSH families. Outline:
- input space $P$
- define a family $\mathcal H = { h \, P \to \mathbb R }$ that maps original datapoint to some real value: $h(\mathbf v) \in \mathbb R$
- next define a family of hash functions $\mathcal G = { g: P \to \mathbb R^k }$ s.t. a $g$ takes $k$ different $h_i \in \mathcal H$ functions:
- $g(\mathbf v) = [ h_1(\mathbf v), h(\mathbf v), \ … \ , h_k(\mathbf v) ] \in \mathbb R^k$
- then take $L$ such $g$ functions from $\mathcal G$: $g_1, g_2, \ … \ , g_L$
Preprocessing:
- store each $\mathbf v \in P$ in bucket $g_j(\mathbf v)$ for all $j = 1 \ .. \ L$
- (can do second hashing to put $g_j(\mathbf v) \in \mathbb R^k$ to a usual Hash Table)
Querying:
- given query $\mathbf q$
- search all buckets $g_1(\mathbf q), g_2(\mathbf q), \ … \ ,g_L(\mathbf q)$
- optional: if number of possible candidates is too large - interrupt after some time, e.g. after first $3L$ items (including duplicates)
- then use linear search to find $k$NN
$k$ and $L$ are parameters chosen s.t.:
- if there exists some $\mathbf v^* \in B(\mathbf q, r_1)$ then $g_j(\mathbf v^*) = g_j(\mathbf q)$ for at least one $g_j$
- total number of collisions on $\mathbf q$ with points from outside $B(\mathbf q, r_1)$ is less than $3L$
A hash function family is ‘‘locality-sensitive’’ if
- “similar” $\mathbf v_1, \mathbf v_2$ - e.g. big $\text{sim}(\mathbf v_1, \mathbf v_2)$ for some Similarity Measure or small $d(\mathbf v_1, \mathbf v_2)$ for some distance measure
- they should collide: have same hash value with high probability
LSH Families
Hamming LSH
- Or Bit Sampling LSH or “the” LSH (Gionis99)
- Approximated distance: Hamming Distance
E2 LSH
- Or p-stable LSH or random projection/quantization LSH
- Euclidean LSH often called E2LSH in the literature
- Approximated Distance: Euclidean Distance
MinHash
- aka Min-Wise independent permutations
- Approximated similarity: Jaccard
SimHash
- http://matpalm.com/resemblance/simhash/
Random Binary Projection
- Approximated similarity: Cosine
- Approximated Distance: Cosine Distance (1 - cosine)
- http://stackoverflow.com/questions/12952729/how-to-understand-locality-sensitive-hashing
- http://www.cs.jhu.edu/~vandurme/papers/VanDurmeLallACL10-slides.pdf
K-Means LSH
- uses the structure of underlying data to find the best hash functions
- “learns” the hash functions via K-Means
Bayesian LSH
- Satuluri, V., Parthasarathy, S. “Bayesian locality sensitive hashing for fast similarity search.” 2012. [http://arxiv.org/abs/1110.1328]
Fewer Hash Tables
Ways to improve LSH
- usually applicable to different LSH Families
Drawback of conventional LSH schemes:
- to guarantee a good quality need to have many hash tables
- it’s a large space requirement for index
- also, in distributed settings it leads to large network load: each hash bucket lookup requires a communication over the network
Hash tables reducing techniques:
- the hash tables occupy a lot of space
- can we have fewer tables but still maintain the same level of performance?
Space requirements:
- each hash table has the same size as the entire dataset (i.e. if dataset has $N$ entries, then the hash index also has $N$ entries)
Entropy LSH
Reduces the number of hash tables
- the indexing (hashing) stage stays the same, but $L$ is smaller than usual
uses different procedure for querying:
- hashes $\mathbf q$ as usual LSH
- but also hashes the query offsets - and sees where the offsets map to
Idea:
- close objects are likely to be in the same bucket as the query - but also in the buckets nearby
- generate query offsets to hit the nearby buckets as well
- this reduces the number of hash tables
But:
- it doesn’t help with network efficiency:
- all $\mathbf q$ + offsets each require a network call
- number of query offsets required by Entropy LSH is larger than the number of hashtables in the original scheme: it’s even less network efficient than usual LSHs
Panigrahy, Rina. “Entropy based nearest neighbor search in high dimensions.” 2006. [http://arxiv.org/abs/cs/0510019]
Multi-Probe LSH
How to increase the quality of LSH?
Probe multiple times
- it increases the scope of search and gives better Precision and Recall
- idea: try to look for hash buckets nearby
Lv, Qin, et al. “Multi-probe LSH: efficient indexing for high-dimensional similarity search.” 2007.
Distributed Layered LSH
Layered LSH
- carefully designed implementation of Entropy LSH
idea:
- distribute hash buckets in such a way that near points are likely to be on the same machine (so get network efficiency)
- while fair away points are likely to be on different machines (so get load balance)
Achieved by rehashing
- rehash the bucket IDs for both data and query via additional layer of LSH
- and then use the hashed buckets as keys
Reference:
- Bahmani, Bahman, Ashish Goel, and Rajendra Shinde. “Efficient distributed locality sensitive hashing.” 2012. [http://arxiv.org/abs/1210.7057]
- there’s a MapReduce implementation and Storm implementation in the paper
Other Meta LSHs
Query-Adaptive LSH
This method adapts its behavior:
- it picks those hash functions that are most likely to return the NN
Usual Query-Adaptive LSH:
- define a pool of $L$ hash functions (with $L$ larger than in usual LSHs)
- compute relevance criteria $\lambda_i$ for each $g_i$: this criteria identifies the hash functions that are more likely to return the NNs
- relevance could be: distance between the query and the center of the cell
Jégou, Hervé, et al. “Query adaptative locality sensitive hashing.” 2008. https://hal.inria.fr/inria-00318614/document
Comparisons
- http://arxiv.org/abs/1206.2082
- minhash vs simhash: Henzinger, Monika (2006), “Finding near-duplicate web pages: a large-scale evaluation of algorithms” [http://infoscience.epfl.ch/record/99373/files/Henzinger06.pdf]
Sources
- Slaney, Malcolm, and Michael Casey. “Locality-sensitive hashing for finding nearest neighbors [lecture notes].” 2008. [http://web.iitd.ac.in/~sumeet/Slaney2008-LSHTutorial.pdf]
- Gionis, Aristides, Piotr Indyk, and Rajeev Motwani. “Similarity search in high dimensions via hashing.” 1999. [http://www.cs.princeton.edu/courses/archive/spring13/cos598C/Gionis.pdf]
- Datar, Mayur, et al. “Locality-sensitive hashing scheme based on p-stable distributions.” 2004. [http://www.cs.princeton.edu/courses/archive/spring05/cos598E/bib/p253-datar.pdf]
- Paulevé, Loïc, et al. “Locality sensitive hashing: A comparison of hash function types and querying mechanisms.” 2010. [https://hal.inria.fr/inria-00567191/document]