Homogeneous Systems of Linear Equations

Homogeneous Linear Systems $A\mathbf x = \mathbf 0$

Suppose we have a system $A\mathbf x = \mathbf 0$. Such a system is called ‘‘homogeneous’’ - because we have $\mathbf 0$ on the right side of the system.

Solving $A\mathbf x = \mathbf 0$

How to solve such a system?

• The solutions to this system form Nullspace $N(A)$
• we can solve it with Gaussian Elimination. The elimination doesn’t change $N(A)$ - the solutions remain the same if we linearly combine the rows
• but note that the elimination changes the Column Space $C(A)$ of $A$

Elimination and Echelon Form

Suppose we have a matrix $A = \begin{bmatrix} 1 & 2 & 2 & 2 \ 2 & 4 & 6 & 8
3 & 6 & 8 & 10
\end{bmatrix}$

• note that row 3 is a linear combination of row 1 and row 2 (the system is not linearly independent)
• while doing the elimination we’ll notice it

Let’s do it:

• $\begin{bmatrix} \boxed 1 & 2 & 2 & 2 \ 2 & 4 & 6 & 8
  3 & 6 & 8 & 10
  \end{bmatrix} \to \begin{bmatrix} \boxed 1 & 2 & 2 & 2 \ 0 & 0 & 2 & 4
  0 & 0 & 2 & 4
  \end{bmatrix}$
• we have 0’s in the second column, but in the next column there’s a non-zero value - can take it as a pivot| |- $\begin{bmatrix} |\boxed 1 & 2 & 2 & 2 \ 0 & 0 & \boxed 2 & 4
  0 & 0 & 2 & 4
  \end{bmatrix} \to \begin{bmatrix} \boxed 1 & 2 & 2 & 2 \ 0 & 0 & \boxed 2 & 4
  0 & 0 & 0 & 0
  \end{bmatrix} = U$
• it’s not really an upper-triangular matrix, but we still can call it $U$
• this $U$ is in the ‘‘echelon form’’ (or “staircase” form)
• 

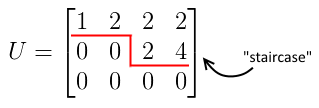
'’rank’’ $r$ of a matrix is the number of Pivot variables in the echelon form

During the elimination the nullspace $N(A)$ of $A$ doesn’t change

• so systems $A\mathbf x = \mathbf 0$ and $U \mathbf x = \mathbf 0$ have the same solutions $\mathbf x$
• the column with pivot variables are called ‘‘pivot columns’’, there are $r$ of them
• the rest of the columns are called ‘‘free columns’’, there are $n - r$ of them
• 

Now let’s try to solve this system $\left{\begin{array}{rl} x_1 + 2 x_2 + 2 x_3 + 2 x_4 & = 0
2 x_3 + 4 x_4 & = 0
\end{array}\right.$

We can find some solutions for pivot variables, but what to do with the free ones?

• They can have any value

• So we may assign something to them and then solve the system with backsubstitution for the pivot variables

• E.g. let’s assign 1 and 0 to $x_2$ and $x_4$
  • we have $\mathbb x = \begin{bmatrix} x_1 \ 1 \ x_3 \ 0 \end{bmatrix}$, then we solve the system and get $\mathbb x = \begin{bmatrix} -2 \ 1 \ 0 \ 0 \end{bmatrix}$
  • we can also take any linear combination of this solution, so we should write $\mathbb x = c_1 \cdot \begin{bmatrix} -2 \ 1 \ 0 \ 0 \end{bmatrix}$
• what if we assign different values to $x_2$ and $x_4$?
  • Can assign this way: $\mathbb x = \begin{bmatrix} x_1 \ 0 \ x_3 \ 1 \end{bmatrix}$, then we solve and get $\mathbb x = \begin{bmatrix} 2 \ 0 \ -2 \ 1 \end{bmatrix}$
  • so we have another “special” solution $\mathbb x = c_2 \cdot \begin{bmatrix} 2 \ 0 \ -2 \ 1 \end{bmatrix}$
• so the final solution to this system will be
  • $\mathbf x = c_1 \cdot \begin{bmatrix} -2 \ 1 \ 0 \ 0 \end{bmatrix} + c_2 \cdot \begin{bmatrix} 2 \ 0 \ -2 \ 1 \end{bmatrix}$
  • this is the Nullspace $N(A)$ of the matrix $A$

Row Reduced Echelon Form

Can we do simpler?

Suppose we have matrix $A$ that we reduced to $U = \begin{bmatrix} \boxed 1 & 2 & 2 & 2 \ 0 & 0 & \boxed 2 & 4
0 & 0 & 0 & 0
\end{bmatrix}$

• can we clean it further? Can try to clean the pivot columns upwards - so there’s only one 1 and the rest are 0’s
• $U = \begin{bmatrix} \boxed 1 & 2 & 2 & 2 \ 0 & 0 & \boxed 2 & 4
  0 & 0 & 0 & 0
  \end{bmatrix} \to \begin{bmatrix} \boxed 1 & 2 & 0 & -2 \ 0 & 0 & \boxed 1 & 4
  0 & 0 & 0 & 0
  \end{bmatrix} = R$
• $R$ is a ‘‘Row Reduced Echelon Form’’ (RRFR) of $A$
• 
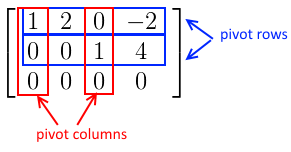
• note that if we consider only the pivot rows and columns, we see that we have the identity matrix $\begin{bmatrix} 1 & 0
  0 & 1
  \end{bmatrix}$

So now if we take a look at our new system, we have

• $\left{\begin{array}{rl} x_1 + 2 x_2 - 2 x_4 & = 0
  x_3 + 2 x_4 & = 0
  \end{array}\right.$
• $A \mathbf x = \mathbf 0$, $U \mathbf x = \mathbf 0$ and $R \mathbf x = \mathbf 0$ - all have the same solutions $\mathbf x$| | | Let’s rearrange columns in $R$ so first we have the pivot columns, and then the free columns
• $\begin{bmatrix} 1 & 0 & 2 & -2 \ 0 & 1 & 0 & 2
  0 & 0 & 0 & 0
  \end{bmatrix}$
• now can distinguish the $I$ part (identity) and the $F$ part (free)
• 

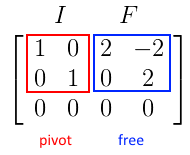
• these $I$ and $F$ appear in the “special” solutions of the $U \mathbf x = \mathbf 0$

  - only $F$ comes with the minus sign: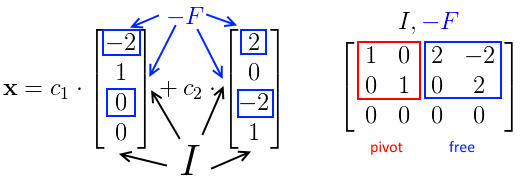

  -

Why does it happen?

• assume we have a RREF $R = \begin{bmatrix} I & F
  0 & 0
  \end{bmatrix}$
• we have $r$ pivot columns, $n-r$ free columns and $r$ pivot rows
• we want to solve $R\mathbf x = \mathbf 0$. What are the “special” solutions?
• let’s create a ‘‘Nullspace matrix’’ $N$, $N = \begin{bmatrix} -F \ I \end{bmatrix}$
• Columns of $N$ are our special solutions
• let’s take a closer look at one of these columns $\begin{bmatrix} \mathop{\mathbf x_\text{pivot}}\limits_\mathop{\mathbf x_\text{free}}\limits_\end{bmatrix}$. The system is $\begin{bmatrix} I & F
  0 & 0
  \end{bmatrix} \cdot \begin{bmatrix} \mathop{\mathbf x_\text{pivot}}\limits_\mathop{\mathbf x_\text{free}}\limits_\end{bmatrix} = \mathbf 0$
• $\Rightarrow$ $I x_\text{pivot} + F x_\text{free} = \mathbf 0$ or $x_\text{pivot} = - F x_\text{free}$
• where for $x_\text{free}$ we use “special” choices $\mathbf e_1, \mathbf e_2, …$ (columns of $I$)

Sources

• Linear Algebra MIT 18.06 (OCW)