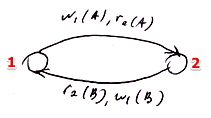ML Wiki

Lock-Based Scheduler

This is a Scheduler that gives Conflict-Serializable Schedule

This scheduler is pessimistic:

• it assumes that something will go wrong, and it's going to prevent that

Notation:

• $w(X)$ - write $X$
• $r(X)$ - read $X$
• $l(X)$ - lock $X$
• $u(X)$ - unlock $X$

Rule:

• before a transaction $T_i$ can read or write a database item $X$, it must obtain the lock on $X$
• if $T_i$ requests a lock that is already taken by other transaction $T_j$, it's paused until $T_j$ releases the lock
• so it's impossible for both $T_i$ and $T_j$ to have a lock on the same database element at the same time

Example

The following is a legal lock-based schedule:

$T_1$	$T_2$
$l_1(A), r_1(A)$
$w_1(A)$
$l_1(B), u_1(A)$
	$l_1(A), r_2(A)$
	$w_2(A)$
$l_2(B)$		lock is denied, $T_2$ pauses
$r_1(B), w_1(B)$
$r_1(B), w_1(B)$
$u_1(B)$		$T_1$ releases $B$, $T_2$ can proceed
	$l_2(B), u_2(A)$
	$r_2(B), w_2(B)$
	$u_2(B)$

Another example:

$S = $

$T_1$	$T_2$
$l_1(A), r_1(A), w_1(A), u_1(A),$
	$l_2(A), r_2(A), w_2(A), u_2(A),$
	$l_2(B), r_2(B), w_2(B), u_2(B),$
$l_1(B), r_1(B), w_1(B), u_1(B)$

Is it conflict-serializable?

• We build a precedence graph:
  • 
• there is a cycle! $\to$ no conflict serializability
• so even if a lock-based schedule is legal, it doesn't mean it's conflict-serializable

Tho-Phase Locking

To get a conflict-serializable schedule:

• for each $T_i$, all lock requests $l_i$ must precede unlock requests $u_i$

In other words

• we can acquire as many locks as you want,
• but then can only unlock them without being able to acquire them again
• $\to$ cannot do $l_i(X), u_i(X), l_i(X), u_i(X)$ within the same transaction $T_i$

$\to$ all locks are released after the entire manipulation with a DB object is completed

• this way the schedule is guaranteed to be conflict-serializable

Theorem

A schedule $S$ obtained by Tho-Phase Locking is conflict-serializable

Proof:

Suppose we have a schedule $S$ in which a transaction doesn't lock after unlocking

• we want to show that we can transform $S$ into a conflict-serializable one by conflict-free swapping

For a schedule with one transaction it's trivial

• assume several transactions

Suppose we have the following schedule:

• $S = ..., w_B(X), ..., u_B(X), ..., l_A(X), ..., u_A(X), ..., r_A(X), ...$
• since $B$ unlocks $X$ there must be $l_B(X)$ that precedes $u_B(X)$
• in this case all actions for element $X$ are performed only by transaction $B$
• by conflict-free swapping can move all actions on $X$ to the front of the schedule
• then remove them and repeat for the remaining elements

$\square$

In Practice

• Transaction manager sends read/write requests
• The scheduler itself inserts locks and unlocks - the transactions don't know anything about them
• Also the locks are usually released after commit
• so if a transaction $T_2$ waits for a lock, it will usually wait until another transaction $T_1$ that keeps the lock commits

Cons and Pros

• Locking is very effective when we have many transactions that both read and write
• When you have few transactions that write it's not efficient - many transactions will have to wait for locks

Other Approaches

There are no problems with two transactions that read at the same time (as long as none of them write)

• there are different kind of locks for that
• Shared Locks - for reading at the same time
• Exclusive Locks - if you also want to write

Also there are hierarchical locks

• locks not on a tuple, but on the whole block

Sources

• Database Systems Architecture (ULB)