Logical Query Plan Optimization
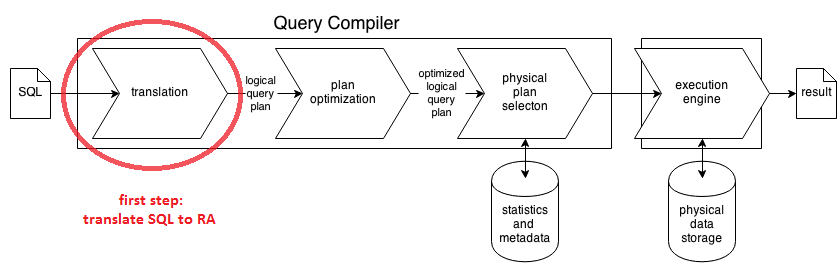
Translating SQL to RA expression is the first step in Query Processing Pipeline
- Input: SQL
- Output: Logical Query Plan - expression in Extended Relational Algebra
Example
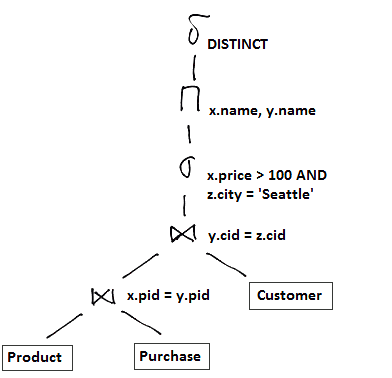
Suppose we have this query
SELECT DISTINCT x.name, z.name
FROM Product x, Purchase y, Customer z
WHERE x.pid = y.pid AND y.cid = z.cid AND
x.price > 100 AND z.city = 'Seattle'
We translate it to the following expression:
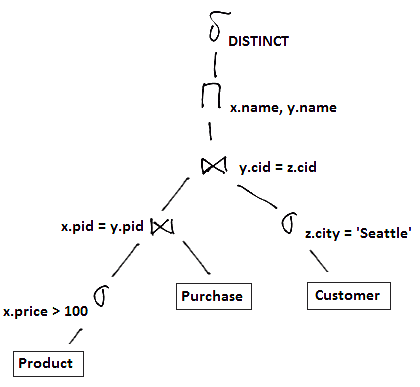
But there is a more optimal way to obtain the same results
The process of finding a cheaper equivalent expression is called (logical) ‘‘query optimization’’
Optimality
- every node needs executing
- hence, the fewer nodes we have, the faster the execution
A Relational Algebra expression $e$ is optimal if there is no other expression $e’$ s.t.
- $e’$ is equivalent to $e$ (i.e. for every database $D:$ $e(D) = e’(D)$)
- $e’$ is shorten (i.e. has fewer operations)
The Optimization Problem
The Optimization Problem
- input: a RA expression $e$
- output: the optimal expression $e’$ s.t. $e \equiv e’$
Undecidability
- This problem in undecidable: on some expressions it may run forever.
- However we can optimize plans of a particular form
Select-Project-Join Expression
In practice, most queries are of the form Select-Project-Join (SPJ)
Example
- $\pi_\text{…} \sigma_{A_1 = B_1 \land … \land A_n = B_n} (R_1 \times … \times R_n)$
- only selections, projections and joins,
- for selections only equalities are used as predicates
And we can optimize this kind of queries| | |
Example
SELECT movieTitle FROM StarsIn S1
WHERE starName IN (
SELECT name
FROM MovieStar, StarsIn S2
WHERE birthdate = 1960
ANDS2.movieTitle = S1.movieTitle)
Note that this query is equivalent to
SELECT movieTitle FROM StarsIn
WHERE starName IN (
SELECT name
FROM MovieStar
WHERE birthdate = 1960)
This one has one join less to execute (and the join is the most expensive operation| ) | |Why?
- the first query may be a result of view expansion (the subquery is actually a view that is expanded for query evaluation)
- careless programmers
It is possible to automatically translate from first kind of query to second one
- the process is called ‘‘removing redundant joins’’
Removing Redundant Joins
The problem:
- given SPJ expression $e$
- eliminate as many joins as possible
- and return equivalent expression $e’$
To do that we could exploit one of the properties of Conjunctive Querys:
- the containment problem (and therefore the equivalence problem) is decidable in them
The algorithm to remove redundant joins is as follows:
- find the minimal Select-Project-Join expression
- translate it to Conjunctive Query
- try removing each atom of the expression and check for equivalence with the original query
- if removing leads to an equivalent query, use it for later checks
- at the end return the simplest version
- it suffices to do a single pass
- once found the optimized CQ query, translate it back to Relational Algebra
This will eliminate the redundant joins in an RA expression
Heuristics
To optimize an RA expression further (after eliminating redundant joins) we can use some heuristics
For relations $R(A, B), S(C, D)$ consider the following expression
- $\pi_A \sigma_{A = 5 \land B < D} (R \times S)$
Pushing Selection
- we want to have selections as close as possible to the actual tables
- so this way we eliminate some tuples before joining them
$\pi_A \sigma_{B < D} \big( \sigma_{A = 5}(R) \times S \big)$
Recognizing Joins
- we replace Cartesian product with Joins
- to help the optimizer assign the best physical operation to this join
$\pi_A \big( \sigma_{A = 5}(R) \Join_{B < D} S \big)$
Introduce Projections
- in this example we see that we need only attribute $D$ in the relation $S$
- so we can introduce projections to save memory
$\pi_A \big( \sigma_{A = 5}(R) \Join_{B < D} \pi_D (S) \big)$
Integrated Exercises
See LQP Optimization Exercises (DBSA)