Quick Sort

Quick Sort

Sorting algorithm based on Divide and Conquer computational paradigm

Advantages:

• $O(n \log n)$
• operates at place

Main idea - partition around a pivot:

• pick an element
• rearrange array so
  • left from pivot => less than pivot
  • right from pivot => greater than pivot

done in $O(n)$ time

<img src=”” >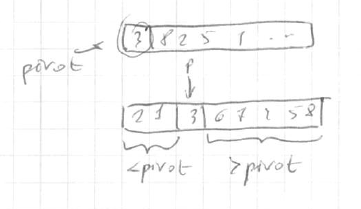

partition:

<img src=”” >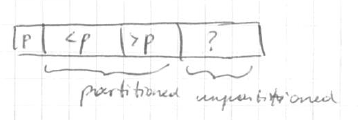

Algorithm

QuickSort(array $A$):

• if $n = 1$ return
• $p$ = ChosePivot($A$, $n$)
• partition $A$ around $p$
• QuickSort(left from $p$)
• QuickSort(right from $p$)

Partition($A$, $l$, $r$):

• // input: $A[l..r]$
• $p = A[l]$
• $i = i + 1$
• for $j = l + 1$ to $r$
  • if $A[j] < p$
    • swap $j$ and $i$
    • $i++$
  • if $A[j] > p$ - do nothing
• swap $l$ and $i - 1$

running time $O(n)$ where $n = r - l + 1$

Pivot

quality

• Running time depends on the quality of pivot
• good quality - always divides into 2 equal halves (matches the median)
• i.e. leads to $\Theta(n)$
• Random pivot is good enough on average cases

So, possible pivots

• 1st element
• last element
• random

Implementation

public void qsort(int[] input, int left, int right) {
    int n = right - left;
    if (n <= 1) {
        return;
    }

    int pivotIndex = partition(input, left, right);

    qsort(input, left, pivotIndex);
    qsort(input, pivotIndex + 1, right);
}

public int partition(int[] input, int left, int right) {
    int pivot = input[left];
    int i = left + 1;

    for (int j = left + 1; j < right; j++) {
        if (input[j] < pivot) {
            swap(input, j, i);
            i++;
        }
    }

    swap(input, left, i - 1);
    return i - 1;
}

public void swap(int[] input, int j, int i) {
    int tmp = input[j];
    input[j] = input[i];
    input[i] = tmp;
}

Randomized Selection ($i$th order statistics)

problem

• input: given $i$th element and array $A$
• goal: find $i$th order statistics (i.e. $i$th smallest element)

Reduction to sorting

• $O(n \log n)$
• apply merge sort
• return $i$th element
• can we do better? yes| | | modification for QuickSort:
• recall Partition procedure
• pivot is on its position| | | how to find $i$th order?
• suppose need 5th element in $A$ of len 10
• after partition, pivot in on 3rd position
• so we need 2nd (5-3) statistics on the $R$ side

Algorithm

RSelect(array $A$, len $n$, order $i$)

• if $n = 1$ return $A[1]$
• choose pivot $p$ from $A$ at random
• partition $A$ around $p$
• $j$ = new index of $p$
• if $j = i$: return $p$ // lucky case
• if $j > i$
  • return RSelect($L$ side of $A$, $j-1$, $i$)
• if $j < i$
  • return RSelect($R$ side of $A$, $n-j$, $i-j$)

Best pivot - the median

• $T(n) \leqslant T(\frac{n}{2}) + O(n)$
• $T(n) = O(n)$

See also

• Divide and Conquer
• Merge Sort

Sources

• Algorithms Design and Analysis Part 1 (coursera)