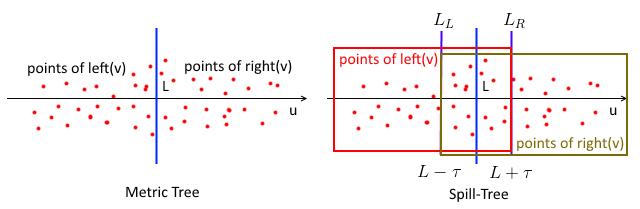
Metric Trees

database-indexing information-retrieval

Metric Trees

Metric tree in an indexing structure that allows for efficient KNN search

Metric tree organizes a set of points hierarchically

It’s a binary tree: nodes = sets of points, root = all points
sets across siblings (nodes on the same level) are all disjoint
at each internal node all points are partitioned into 2 disjoint sets

Notation:

let $N(v)$ be all points at node $v$
$\text{left}(v), \text{right}(v)$ - left and right children of $v$

Splitting a node:

choose two pivot points $p_l$ and $p_r$ from $N(v)$

ideally these points should be selected s.t. the distance between them is largest:

$(p_l, p_r) = \operatorname{arg max}\limits_{p_1, p_2 \in N(v)} | p_1 - p_2 |$

- but it takes $O(n^2)$ (where $n =

N(v)

$) to find optimal $p_l, p_r$

- heuristic:

pick a random point $p \in N(v)$
then let $p_l$ be point farthest from $p$
and then let $p_r$ be point farthest from $p_l$

once we have $(p_l, p_r)$ we can partition:
- project all points onto a line $u = p_r - p_l$
- find the median point $A$ along the line $u$
- all points on the left of $A$ got to $\text{left}(v)$, on the right of $A$ - to $\text{right}(v)$
- by using the median we ensure that the depth of the tree is $O(\log N)$ where $N$ is the total number of data points
- however finding the median is expensive
heuristic:
- can use the mean point as well, i.e. $A = (p_l + p_r) / 2$
let $L$ be a $d - 1$ dimensional plane orthogonal to $u$ that goes through $A$
- this $L$ is a ‘‘decision boundary’’ - we will use it for querying

After metric tree is constructed at each node we have:

the decision boundary $L$
a sphere $\mathbb B$ s.t. all points in $N(v)$ are in this sphere
- let $\text{center}(v)$ be the center of $\mathbb B$ and $r(v)$ be the radius
- so $N(v) \subseteq \mathbb B\big(\text{center}(v), r(v)\big)$

’'’MT-DFS’’’($q$) - the search algorithm

search in a Metric Tree is a guided Depth-First Search
the decision boundary $L$ at each node $n$ is used to decide whether to go left or right
- if $q$ is in the left, then go to $\text{left}(v)$, otherwise - to $\text{right}(v)$
- (or can project the query point to $u$, and then check if $q < A$ or not)
all the time we maintain $x$: nearest neighbor found so far

let $d = | x - q |$ - distance from best $x$ so far to the query

- we can use $d$ to prune nodes: we can check if a node is good or no point can better than $x$

no point is better than $x$ if $| \text{center}(r) - q | - r(v) \geqslant d$

This algorithm is very efficient when dimensionality is $\leqslant 30$

but slows down when it increases

Observation:

MT often finds the NN very quickly and then spends 95% of the time verifying that this is the true NN
can reduce this time with Spill-Trees

Spill-Trees

A Spill-Tree is a variant of Metric Tree

in which children of a node can “spill over” onto each other
i.e. $\text{left}(v)$ and $\text{right}(v)$ are no longer required to be disjoint

Partitioning

the decision boundary $L$ still goes though $A$
but we define two additional separate planes $L_L$ and $L_R$
let $\tau$ be the area that both left and right children of $v$ can share
$L_L = L - \tau$ and $L_R = L + \tau$
- $\tau$ is the size of overlap
then $\text{left}(v)$ contains all points on the left of $L_R$ and $\text{right}(v)$ contains all the points on the right of $L_L$
illustration:

Why allowing overlap?

find the answer approximately, not exactly

’'’SP-Search’’’($q$)

don’t backtrack at all - just do a tree descent, not DFS
consider a case when $q$ is close to $L$: it’s true that the true NN might be on the other side of $L$
so by allowing overlap we hope to catch the true NN on the over side
and by varying $\tau$ we can reduce the probability of a mistake

Hybrid Spill-Trees

Problems with Spill-Trees: depth varies a lot with $\tau$

Construction

let $\rho < 1$ be the balance threshold (usually $\rho = 0.7$)

Similar to SP-Trees, but

if either of $v$’s children contains more than $\rho \cdot

N(v)

$ elements

- then don’t do overlapping nodes - use usual MT split and mark the node as “non-overlapping”

this way we still can maintain the logarithmic depth

Search:

also hybrid of both
if non-overlapping: do backtracking
if overlapping: don’t backtrack

Random Projections: Dimensionality Reduction

Both SP and MT aren’t very efficient for $D \geqslant 30$

but by Johnson-Lidenstrauss Lemma (see Achlioptas2003) know that
- we can always embed $N$ points into a subspace with dimensionality $\log N$
- with little distortion on pair-wise distances.
so let’s do a very simple embedding: Random Projections
pick up a random subspace $S$ and project all data on $S$

So,

do Random Projection as a preprocessing step: project all data points on $S$ and build the tree on the low dimensional representation
by doing projection we’ll lose some accuracy
can fix that by doing multiple different random projections and do a hybrid search for each resulting tree separately
if probability of failing to find the true NN is $\delta$, then do doing $L$ different projections we reduce this probability to $\delta^L$

References

Uhlmann, Jeffrey K. “Metric trees.” 1991. [http://trac.astrometry.net/export/20934/trunk/documents/papers/dstn-review/papers/uhlmann1991b.pdf]
Omohundro, Stephen M. “Bumptrees for efficient function, constraint, and classification learning.” 1991. [http://www1.icsi.berkeley.edu/ftp/pub/techreports/1991/tr-91-009.pdf]
Achlioptas, Dimitris. “Database-friendly random projections: Johnson-Lindenstrauss with binary coins.” 2003. [http://www.sciencedirect.com/science/article/pii/S0022000003000254]

Sources

Liu, Ting, et al. “An investigation of practical approximate nearest neighbor algorithms.” 2004. [http://machinelearning.wustl.edu/mlpapers/paper_files/NIPS2005_187.pdf]

✏️ Edit on GitHub