Motivation: Searching
Suppose we have a relation $R(A, B, C, D)$, each tuple - 32 bytes
- $128 \times 10^6$ tuples is $R$
- Block size is $B$ = 4kb
- I.e. can store 128 tuples per block, $10^6$ tuples in total
Suppose we want to find a tuple with $C = 10$
Searching in I/O Model of Computation
- for each block $X \in R$
- load $X$
- check if there’s a tuple $T \in X$ with $C = 10$
- yes - output $T$
- no - continue
- release $X$ from memory
In worst case it’s $10^6$ I/Os
- suppose $10^{-3}$ seconds per I/O operation
- 16.6 minutes in total
Can we do better?
Indexing
An ‘‘index’’ is any secondary memory data structure that
- takes a search key as input
- efficiently returns the collection of matching records
One-Dimensional Indexes
Conventional Indexes
- Dense Index
- Sparse Index
- Secondary Index as a combination of both
Tree-Based Indexes
Hash-Based Indexes
Multi-Dimensional Indexes
Conventional
Tree-Based Indexes
Hash-Based Indexes
Clustered Index
Index can be clustered or unclustered
- When index is clustered it means the records themselves are stored in index, not pointers
- I.e. a clustered index ensures that all data is stored in some order
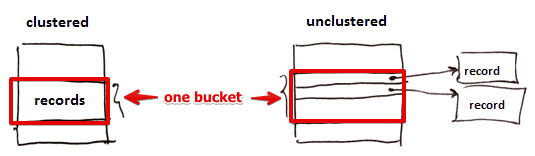
- Usually there is only one clustered index per relation (otherwise the data will be duplicated)
If an index (say, B-Tree) is not clustered, then instead of following each pointer other techniques can be used, such as Bitmap Heap Scan
Information Retrieval Indexing
Indexing can also be applied to unstructured data such as text
- Inverted Index builds an index from words to documents where these words are contained
- Locality Sensitive Hashing gives an approximate answer to KNN queries
Sources
- Database Systems Architecture (ULB)
- Database Systems: The Complete Book (2nd edition) by H. Garcia-Molina, J. D. Ullman, and J. Widom