ML Wiki
Machine Learning Wiki - A collection of ML concepts, algorithms, and resources.

Non-Deterministic Finite Automata

automata

Non-Deterministic Finite Automata

Automata that are ‘‘non-deterministic’’ (NFA) can be in several states at once

  • from a state $q$ on input $a$ it can go to several different states
  • so there are several transitions that are labeled $a$
  • this is why it’s called non-deterministic
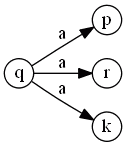
  • Image
  • it also has one start state and several final states
  • it accepts a sequence if any of the choices lead to one of the final states
  • so when there are choices where to go, a NFA tries all

Definition

Formally, a Non-Deterministic Finite Automata $A$ is a tuple $A = \langle Q, \Sigma, \delta, q_0, F \rangle$

  • $Q$ is a set of states
  • $\Sigma$ - input alphabet
  • $\delta$ - transition functions (returns a set of transitions)
  • $q_0 \in Q$ - the start state
  • $F \subseteq Q$ - the final states

A string $w$ is accepted if

  • $\exists p \in \delta(q_0, w): p \in F$

The ‘‘language’’ $L(A)$ of $A$

  • is the set of all strings it accepts
  • languages defined by NDA are also Regular Languages

Transition Function

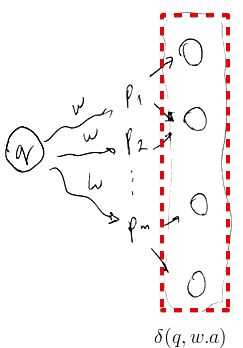
Unlike in DFAs, $\delta(q, a)$ returns a set of states

  • $\delta(q, a) = { p_1, …, p_m } $
  • and it can return an empty set $\varnothing$ if there’s nothing to go next

Extension to strings (i.e. Extended $\delta$) is a bit more complex than for DFA

  • basis:
    • $\delta(q, \epsilon) = { q }$
    • the only state you can reach on empty input is the state $A$ is in
  • induction
    • $\delta(q, w . a) = \bigcup_{p \in \delta(q, w)} \delta(p, a)$
    • i.e. union of all $\delta(p, a)$ for all $p$ reachable with a word $w$
    • Image

Example 1

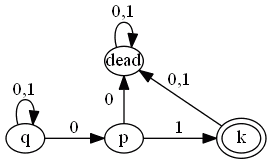| Image || | | | | 0 | 1 | | $\to$ | $q$ | | $ { p, q } $ | $ { q } $ | | | | $p$ | | dead | ${ k }$ | | | | $k$ | | dead | dead | | | | dead | | dead | dead |

  • in $q$ on 0 it can stay in $q$ or go to $p$

Suppose the word is $w = 0001$

  • Image
  • the only possible run is $qqqpk$

But since NDA are non-deterministic

  • we know it will always make a good choice
  • so we don’t need “dead” transitions - we can just reject strings when there’s nothing to go next
  • and we can have something like the following
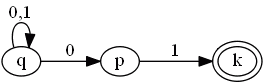Image           0 1   $\to$ $q$   $ { p, q } $ $ { q } $       $p$   $\varnothing$ ${ k }$       $k$   $\varnothing$ $\varnothing$

the alphabets of these two automata are the same

Example 2

  • consider this chessboard of size 3 $\times$ 3
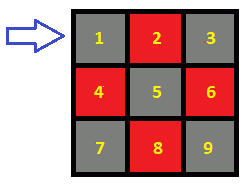
  • Image
  • states = squares of the chessboard
    • $Q = {1, 2, 3, 4, 5, 6, 7, 8, 9}$
  • $\Sigma = { r, b }$
    • $r$ - “red” move: you move to any adjacent red square
    • $w$ - “black” move: you move to any adjacent black square
  • start state - left upper corner
    • $q_0 = 1$
  • final state - lower right corner
    • $F = { 9}$

Consider this sequence: $rbb$

  • there are many possible ways to execute this sequence
  • try each
  • Image
  • we see that the final state is reached - so this sequence is accepted

DFA vs NFA

DFA is NFA without non-determinism

  • so a DFA $A_D$ can easily be turned into an NFA $A_N$ that accepts the same language
  • if $\delta_D(q, a) = p$ then let $A_N$ have $\delta_N(q, a) = { p } $
  • and $L(A_D) \equiv L(A_N)$

But also for any NFA $A_N$ there exists DFA $A_D$ s.t.

  • $L(A_N) \equiv L(A_D)$
  • thus, NFAs also define Regular Languages
  • can show that by ‘‘subset construction’’

Subset Construction

Problem statement:

  • Given NFA $A_N = \langle Q, \Sigma, \delta_N, q_0, F \rangle$
  • construct DFA $A_D = \langle 2^Q, \Sigma, \delta_D, { q_0 }, F’ \rangle$ where
    • $2^Q$ is a powerset of $Q$ - set of all subsets from $Q$
    • input alphabet $\Sigma$
    • transition function $\delta_D$
    • start state ${ q_0 }$
    • finals states $F’ = { q_F \ \ q_F \in 2^Q: \exists q \in F }$ - all possible subsets of $Q$ that contain at least one state from the set of final states $F$ from NFA $A_N$
  • such that $L(A_N) \equiv L(A_D)$

Note:

  • states of $A_D$ have names that look like set of states (e.g. ${g_0}$ or $ {q_1, q_2, q5} $)
  • however they are single objects
    • this is just a naming convention to show that one state in $A_N$ may correspond to multiple states of the NFA
  • so an expression like ${p, q}$ must be understood by DFA as a single symbol, not as a set

Next, we define the transition function $\delta_D$ as

  • $\delta_D( \underbrace{{q_1, …, q_k}}\text{a state of DFA} , a) = \bigcup{i = 1}^k \delta_N (q_i, a)$
  • so for a state ${q_1, …, q_k}$ in $A_D$ for all $q_i$ from this state
    • we take a union over possible next states from $A_N$

Problem:

  • the number of states in DFA is exponential to $ Q $ - so it may also be very expensive to transform NFA to DFA
  • it gets very hard to visualize

Example

Recall the chessboard NFA

Image         State   $r$ $b$   $\to$ 1 ${ 2,4 }$ ${ 5 }$     2 ${ 4,6 }$ ${ 1,3,5 }$     3 ${ 2,6 }$ ${ 5 }$     4 ${ 2,8 }$ ${ 1,5,6 }$     5 ${ 2,4,6,8 }$ ${ 1,3,7,9 }$     6 ${ 2,8 }$ ${ 3,5,9 }$     7 ${ 4,8 }$ ${ 5 }$     8 ${ 4,6 }$ ${ 5,7,9 }$   $*$ 9 ${ 6,9 }$ ${ 5 }$

Let’s construct a DFA for it

  • we’ll do a ‘‘lazy’’ construction of DFA states:
    • that is, instead of generating all elements of $A^Q$ we will add only needed ones on the go
  State   $r$ $b$ $\to$   ${ 1 }$ ${ 2,4 }$ ${ 5 }$       ${ 2,4 }$ ${ 2,4,6,8 }$ ${ 1,3,5,7 }$       ${ 5 }$ ${ 2,4,6,8 }$ ${ 1,3,7,9 }$       ${ 2,4,6,8 }$ ${ 2,4,6,8 }$ ${ 1,3,5,7,9 }$       ${ 1,3,5,7 }$ ${ 2,4,6,8 }$ ${ 1,3,5,7,9 }$   $*$   ${ 1,3,7,9 }$ ${ 2,4,6,8 }$ ${ 5 }$   $*$   ${ 1,3,5,7,9 }$ ${ 2,4,6,8 }$ ${ 1,3,5,7,9 }$

The way of doing it:

  • in NFA, on $r$ from state 2 we can get to ${ 4,6 }$, from 4 - to ${ 2,8 }$
    • so for the DFA, on $r$ from state $ { 2,4 } $ we can go to state ${ 4,6 } \cup { 2,8 } \equiv { 2,4,6,8 }$
    • we see if there’s already such state in the table - it no, we create it, otherwise use the existent one

Note that in this case it has even fewer states than the original one

  • but it’s rarely the case

Proof of Equivalence

$\forall w: w \in L(A_N) \iff w \in L(A_D)$

Here we can show that

  • $\forall w: \delta_N(q_0, w) \equiv \delta_D( {q_0}, w)$
  • i.e. for any word $w$ we get to the same state
  • (recall that $\delta_N(q_0, w)$ returns a set, and $\delta_D( {q_0}, w)$ returns a state which also can be seen as a set)

Proof by induction on $| w |$ |- IH: $\delta_N(q_0, w) \equiv \delta_D( {q_0}, w)$

  • basis: $w = \epsilon$
    • $\delta_N(q_0, \epsilon) \equiv \delta_D( {q_0}, \epsilon) \equiv {q_0}$
  • induction step
    • let $w = x.a$, the IH holds for $x$ (by induction)
    • let $S = \delta_N(q_0, x) \equiv \delta_D( {q_0}, x)$
    • and let $T$ be $T = \bigcup_{p \in S} \delta_N (p, a)$
    • Image
    • then by construction of $A_D$ we see that
      • $\delta_N(q_0, w) \equiv \delta_D( {q_0}, w) \equiv T$
      • (refer to Subset Construction and the extension rule of NDA)

$\square$

$\epsilon$-Transitions

We can allow state-to-state transitions on empty input $\epsilon$

  • these transitions are done spontaneously, without looking at the input string
  • but still with these transitions we can accept only Regular Languages

NFAs with $\epsilon$-Transitions

Consider this example

  • the arcs labeled with $\epsilon$ can be followed at any time without taking anything from the input sequence
  • in a transition table we have an additional column for $\epsilon$-transitions
  • but $\epsilon$ is not an input symbol, and $\epsilon \not \in \Sigma$
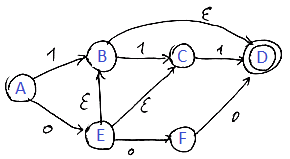Image           0 1 $\epsilon$   $\to$   $A$   ${ E }$ ${ B }$ $\varnothing$       $B$   $\varnothing$ ${ C }$ ${ D } $       $C$   $\varnothing$ ${ D }$ $\varnothing$   $*$   $D$   $\varnothing$ $\varnothing$ $\varnothing$       $E$   ${ F }$ $\varnothing$ ${ B,C } $       $F$   ${ D }$ $\varnothing$ $\varnothing$

Have a look on $E$:

  • there are two $\epsilon$-transitions to $B$ and $C$
  • so it can go to $B$ spontaneously and then to $D$
  • on input 1 it can to $B$ and there to $C$
  • or to $C$ and there to $D$
  • so there are quite a few nodes that are directly reachable from $E$
  • this leads us to the notion of ‘‘closure’’ of $E$

Closure of States

The closure of a state $q$, denoted $\text{CL}(q)$, is

  • the set of all states that you can get from $q$
  • following only $\epsilon$-transitions

Image

  • in this example, $CL(E) = { B, C, D, E }$
    • from $E$ you can get to $B$ and $C$, and from $B$ to $D$
  • for $A$ there are no $\epsilon$-transitions, so $\text{CL}(A) = { A} $
    • (on $\epsilon$ you can stay in $A$)

The closure $\text{CL}(S)$ of a set of states $S = { q_1, …, q_k }$

  • is the union of closures of each $q_i$
  • $\text{CL}(S) = \bigcup_{q_i \in S} \text{CL}(q_i)$

Extended $\delta$

Intuition:

  • $\hat{\delta}(q_0, w)$ is the set of states that you can reach from the initial state $q_0$ following a path labeled $w$
  • remember that $\epsilon$ are invisible, so in $w$ there are only real input seen by the automaton
  • but spontaneously at any moment whenever possible it can follow an $\epsilon$ transition

Definition of $\hat{\delta}(q_0, w)$

  • basis: $\hat{\delta}(q_0, w) = \text{CL}(q_0)$
  • induction: input is $w = x.a$
    • $\hat{\delta}(q_0, x) = S$ set of states reachable with $x$
    • $\forall p \in S$ take the union of $\text{CL}(\delta(p, a))$
    • so $\hat{\delta}(q_0, x.a) = \bigcup_{p \in \hat{\delta}(q_0, x)} \text{CL}(\delta(p, a))$

Illustration

  • suppose $x \equiv bc$
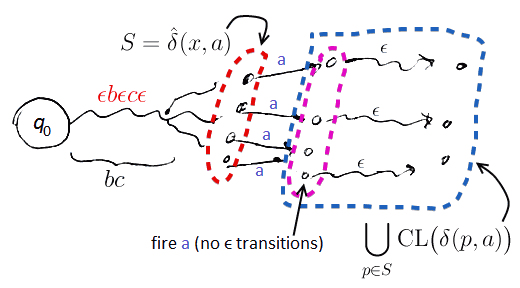
  • Image
  • we start from $q_0$
    • then follow all $\epsilon$-transitions
    • then follow $b$
    • then again all $\epsilon$-transitions
    • then $c$
    • and again $\epsilon$-transitions
  • let $S$ be the set of reachable states from $q_0$ on word $x$
    • i.e. $S \equiv \hat{\delta}(q_0, x) \equiv \hat{\delta}(q_0, bc)$
  • now from $S$ we fire all $a$ transitions (no $\epsilon$ yet)
  • and then we take the closure of this set $S$

Example

  • Image
  • $\hat\delta(A, \epsilon) = \text{CL}(A) = { A } $ (the basis rule)
  • $\hat\delta(A, 0) = \text{CL}({ E }) = { B,C,D,E } $
    • the only place we can get from $A$ on 0 is ${ E }$
    • but we close on $E$ and get to ${ B,C,D } $
  • $\hat\delta(A, 01) = \text{CL}({ C,D }) = { C,D } $
    • on 0 we can get to ${ B,C,D,E } $
    • but only in ${ B,C } $ we can have 1
    • and from ${ B,C } $ we can get only to ${ C,D } $

Language of $\epsilon$-NFA

The language of $\epsilon$-NFA is

  • the set of strings $w$ s.t. $\hat\delta(q_0, w) \cap F \not \equiv \varnothing$
  • i.e. it’s possible to get on $w$ to at least one of the final states from $F$
  • languages defined by $\epsilon$-NFAs are also Regular Languages

Equivalence of NFA and $\epsilon$-NFA

  • Every NFA is an $\epsilon$-NFA, but without $\epsilon$-transitions
    • $\Rightarrow$ $\forall$ NFA $A_N$ there $\exists$ $\epsilon$-NFA $A_\epsilon$ that accepts the same language
    • $L(A_N) \equiv L(A_\epsilon)$
  • but showing the other way - that $\forall A_\epsilon \ \exists A_N: L(A_\epsilon) \equiv L(A_N)$ - is harder
    • we need to remove $\epsilon$-transitions

Algorithm

  • given $\epsilon$-NFA $A_\epsilon = \langle Q, \Sigma, q_0, F, \delta_\epsilon \rangle$
  • and an “ordinary” NFA $A_N = \langle Q, \Sigma, q_0, F’, \delta_N \rangle$
  • compute $\delta_N(q, a)$ as
    • let $S = \text{CL}(q)$
    • and $\delta_N(q, a) = \bigcup_{p \in S} \delta_\epsilon(p, a)$
    • all states that can be reaches from $q$ on $a$ and $\epsilon$ in $A_\epsilon$ (or, from $\text{CL}(q)$) in the $A_N$ can be reached only on $a$
  • and define $F’$ as
    • it’s a set of states $q$ s.t. $\text{CL}(q) \cap F \not \equiv \varnothing$
    • if the $\epsilon$-NFA can get to a final state by following an $\epsilon$-transitions, we make such state final in the NFA as well
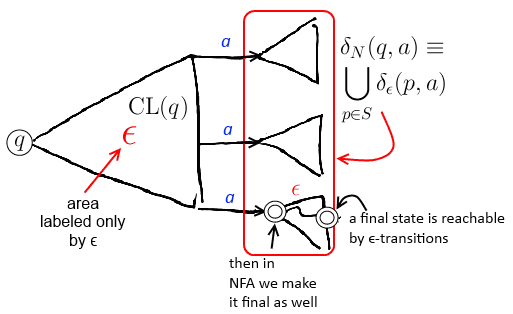
  • Image

These construction gives an equivalent NFA

  • on $w$ the NFA $A_N$ will enter the same set of states that $A_\epsilon$ would enter on $w$
  • so by induction on $ w $ need to show that $\text{CL}( \delta_N (q_0, w) ) = \hat\delta(q_0, w)$

Example

Consider again this $\epsilon$-NFA:

Image           0 1 $\epsilon$   $\to$   $A$   ${ E }$ ${ B }$ $\varnothing$       $B$   $\varnothing$ ${ C }$ ${ D } $       $C$   $\varnothing$ ${ D }$ $\varnothing$   $*$   $D$   $\varnothing$ $\varnothing$ $\varnothing$       $E$   ${ F }$ $\varnothing$ ${ B,C } $       $F$   ${ D }$ $\varnothing$ $\varnothing$

The equivalent NFA without $\epsilon$-transitions is the following:

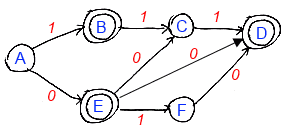Image           0 1   $\to$   $A$   ${ E }$ ${ B }$   ${\color{blue}{*}}$   $B$   $\varnothing$ ${ C }$       $C$   $\varnothing$ ${ D }$   $*$   $D$   $\varnothing$ $\varnothing$   ${\color{blue}{*}}$   $E$   ${ F }$ ${ C, D }$       $F$   ${ D }$ $\varnothing$

Transformation

  • Here are two interesting closures:
    • $\text{CL}(B) = { B, D}$
    • $\text{CL}(E) = { B,C,D, E}$
  • first, we need to change the transition on 1 from $E$
    • $\text{CL}(E) = { B,C,D, E}$
    • where we can get from these states on 1?
    • to ${ C,D }$
    • so we put this set for $E$ on 1
  • Translation on 0 from $E$ doesn’t change
    • we don’t have any transitions on 0 from ${ B,C,D, E}$
    • only ${ F }$, which is already there
  • Since closures of $B$ and $E$ contain the final state $D$, they also become final

Summary

✏️ Edit on GitHub