Deterministic Finite Automata
Deterministic Finite Automata (DFA) are Automata that defile Regular Languages
Formal Languages
A ‘‘language’’ $L$ is a subset of all possible words $\Sigma^*$ formed by symbols of alphabet $\Sigma$
- English, French
- words with equal number of 1’s and 0’s
- and so on
Informal Introduction
A ‘‘finite automata’’ is a formal system
- it can be viewed as a graph or table
- it remembers only finite amount of information
- it has only finite number of states
- states chance in response to some input: characters or events
- rules that tell how the state changes are called ‘‘transitions’’
Usage:
- design and verification of circuits and communication protocols
- text-processing applications (Regular Expressions)
- very important for creating compilers
Definition
A ‘‘Deterministic Finite Automaton’’ (DFA) is a tuple $A = \langle Q, \Sigma, \delta, q_o, F \rangle$
- $Q$ is a finite set of states
- $\Sigma$ a finite input alphabet
- $\delta$ a transition function
- $q_0 \in Q$ - the start state
- $F \subseteq Q$ - the final (or “accepting”) states
Transition Function
'’Transition function’’ $\delta$
- a function $\delta(q, a)$ that takes
- the current state of $q \in Q$ of $A$
- the current input symbol $a \in \Sigma$
- and returns the next state where $A$ goes
- $\delta$ defines a total relation: $\forall q, a \ \exists p: \delta(q, a) = p$
- for DFA there for each pair $(q, a)$ there exists exactly one state $p$ (for deterministic behavior)
A ‘‘dead state’’:
- a state that is not final, but there’s no way to escape it
- on every input symbol there’s a transition to itself
- once you get there, it’s not possible to leave it
Extended Transition Function
Extended Transition Function $\delta$ (sometimes $\hat{\delta}$) is
- a function that takes $q$ and a ‘'’word’’’ $w$ (of any length, including 0)
- and tells where the automaton $A$ gets to after applying this word $w$
- i.e. it follows the path from $q$ by arcs labeled by symbols from $w$ in order
Inductive definition of extended $\delta$:
- basis
- $\delta(q, \epsilon) = q$
- if you’re in state $q$ and see no symbols, you stay in the state $q$
- induction
- $\delta(q, w.a) = \delta(\delta(q, w), a)$
- $w$ is string, $a$ is symbol, $.$ is concatenation
- state we end up after seeing $wa$ is state $q’$ after seeing $w$ plus $\delta(q’, a) $
A ‘‘run’’ of a string $w = a_1 . \ … \ . a_n$ on automaton $A$
- is the sequence of state changes that $A$ makes while executing $w$
Representation: Graph
It is possible to represent automata as Graphs
- nodes = states of automaton
- arcs $(p, q)$ represent transitions, they are labeled by symbols that lead from $p$ to $q$
- arrow labeled with “start” denotes the start state
 $\iff$ $\delta(p,a) = \delta(p,b) = q$
$\iff$ $\delta(p,a) = \delta(p,b) = q$
Example 1
- recognizing if a word ends with “ing”
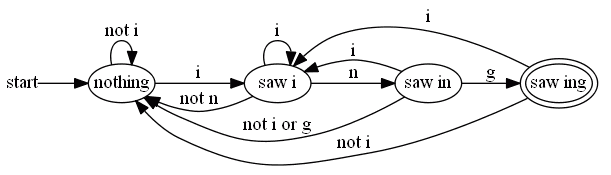
- “nothing” represents a state where we’ve made no progress towards “ing”
- $i$ in input - go to “saw i”, otherwise stay
- “saw i” means that $i$ was the last seen symbol
- see $n$ - made progress towards “ing” and go to “saw in”
- saw another $i$ - say here (maybe the word is “skiing”)
- “saw in”
- go to “saw ing” on $g$
- return on other symbols
- “saw ing” - nothing in the input - we won
- something: return either to “saw i” or “nothing”
Example 2
- $\Sigma = {0, 1} $
- recognizes strings with no 11

- $C$ is a dead state: once saw 11 - we are not going to accept this string
Example 3: Tennis
Rules:
- Match consists of 3-5 sets, a set of 6 or more games
- one person servers throughout a whole game
- to win, a player must score at least 4 points, but win by at least 2 points
Symbols:
- $s$ = “server wins a point”
- $o$ = “opponent wins a point”
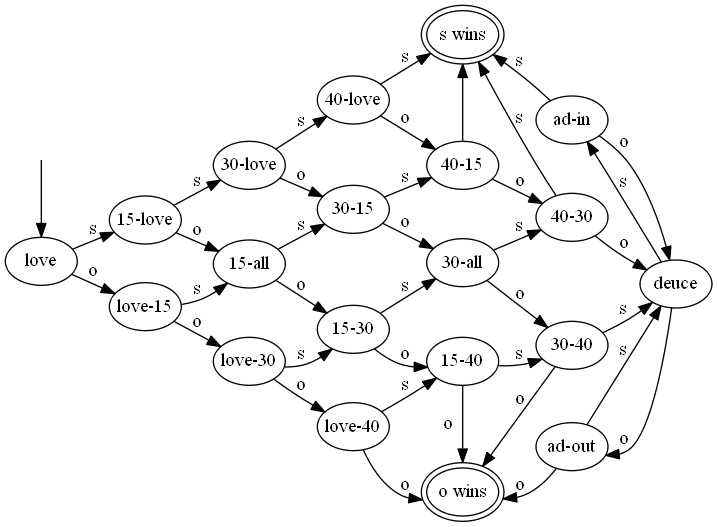
Game:
- it starts from the ‘'’love’’’ state: both players have 0-0
- at each state, depending on who wins, we transition from one state to another
- note: for “15-all” - we don’t know how exactly we got there, but it doesn’t matter
- final states are when somebody wins
- “deuce” - when there’s a tie
- note that it remembers that there’s a tie,
- but it doesn’t remember how many points have been played
- after this state you have to win by 2 points
- advantage-in, advantage-out - the names of these intermediate states between deuce and winning
Consider this sequences of points:
- $sosososososs$
- we’ll obtain the following run:

Representation: Table
It is also possible to represent an automaton with a table
- $\to$ indicates start
- $*$ indicates final states
- rows are states
- columns are input symbols
- the cells shows transitions
 $\Huge \equiv \ $ $\Huge \equiv \ $ |
0 | 1 | $\to$ | $*$ | A | A | B | $*$ | B | A | C | C | C | C |
Language of DFA
Automata define Formal Languages
- if $A$ is an automaton, $L(A)$ is its language
- for a DFA $A$, $L(A)$ is a set of strings that lead from the start state $q_0$ to one of the final states $F$
- formally: $L(A) = { \forall w : \delta{q_0, w} \in F }$
- languages defined by Finite Automata are called Regular Languages
Non-Deterministic Finite Automata
In Non-Deterministic Finite Automata (NFAs) one input can lead to multiple states
- additionally there can be $\epsilon$-transitions that can taken spontaneously without any input character
- it is possible to convert one representation to another
- thus they all define the same class of Formal Languages: Regular Languages
- Non-Determinism and $\epsilon$-transitions give additional power
- NFAs are easier to design than DFAs
- but only DFAs can be implemented in practice
-
Computers are always deterministic
-