ML Wiki

One vs All Classifier

Suppose we have a classifier for sorting out input data into 3 categories:

• class 1 ($\triangle$)
• class 2 ($\square$)
• class 3 ($\times$)

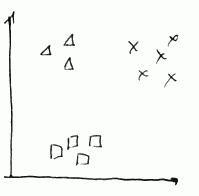
We may turn this problem into 3 binary classification problems (i.e. where we predict only $y \in \{0, 1\}$) to be able to use classifiers such as Logistic Regression.

• We take values of one class and turn them into positive examples, and the rest of classes - into negatives

• Step 1
  • triangles are positive, and the rest are negative - and we run a classifier on them.
  • 
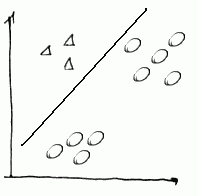
  • and we calculate $h_{\theta}^{(1)}(x)$ for it
• Step 2
  • next we do same with squares: make them positive, and the rest - negative
  • 
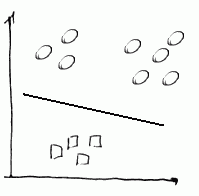
  • and we calculate $h_{\theta}^{(2)}(x)$
• Step 3
  • finally, we make $\times$s as positive and the rest as negative and calculate $h_{\theta}^{(3)}(x)$
  • 

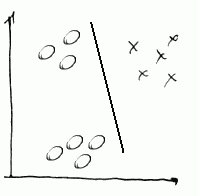
So we have fit 3 classifiers:

• $h_{\theta}^{(i)}(x) = P(y = i | x; \theta), i = 1, 2, 3$
• Now, having calculated the vector $h_{\theta}(x) = [h_{\theta}^{(1)}(x), h_{\theta}^{(2)}(x), h_{\theta}^{(3)}(x)]$ we just pick up the maximal value
• i.e. we choose $\max_{i} h_{\theta}^{(i)}(x)$

Implementation

The implementation is straightforward

• Matlab/Octave implementation can be found here

Sources

• Machine Learning (coursera)