Motivation
Suppose we have a ‘‘binary classification problem’’:
- $y \in {0, 1}$ -
- 0 - negative class, connected with absence of smth (not spam)
- 1 - positive class, connected with presence of smth (spam)
Linear Regression
We may try to use Linear Regression for that
-
- We fit a regression line
- $h_{\theta}(x) = \theta^T x$
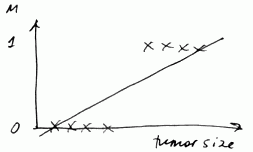
- And we set a “threshold” at 0.5
- if $h_{\theta}(x) \geqslant 0.5$ - we predict 1
- if $h_{\theta}(x) < 0.5$ - we predict 0
What’s wrong with this approach?
- Linear regression is susceptible to outliers - a single outlier can break the classificator
- $h_{\theta}(x)$ can be $> 1$ or $< 0$
- So linear regression is not a good idea
We need to develop something that outputs values from range $[0, 1]$ that we can treat as probabilities
Logistic Regression
Logistic Regression - is a classification algorithm
Hypothesis Representation
- we want - $0 \leqslant h_{\theta}(x) \leqslant 1$
- let $h_{\theta}(x) = g(\theta^T x)$
-
- where $g(z) = \cfrac{1}{1 + e^{-z}}$ - ‘‘sigmoid (logistic) function’’
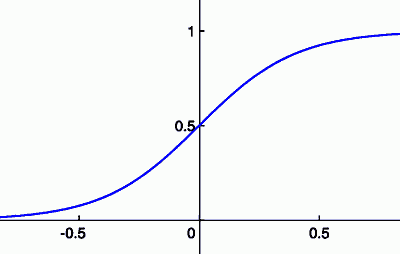
- it’s always between 0 and 1
It inputs probability
- We interpret the output from $h_{\theta}(x) $as probability that $y = 1$ on input $x$, or
-
$h_{\theta}(x) = P(y = 1 x; \theta)$: probability that $y = 1$ given $x$ parametrized by $\theta$ - As $y = {0, 1}$, $P(y = 0 x; \theta) = 1 - P(y = 1 x; \theta)$
For example, suppose $x = \left[\begin{matrix} x_0 \ x_1 \end{matrix} \right] = \left[\begin{matrix} 1 \ \text{tumor size} \end{matrix} \right]$
- if $h_{\theta}(x) = 0.7$, there’s 70% chance of tumor being malignant
Decision Boundary
Suppose we predict
- “$y = 1$” if $h_{\theta}(x) \geqslant 0.5$, and
-
“$y = 0$” if $h_{\theta}(x) < 0.5$
-
- $g(z) \geqslant 0.5$ when $z \geqslant 0$

- so $h_{\theta}(x) = g(\theta^T x) \geqslant 0.5$ when $\theta^T x \geqslant 0$
Decision Boundary Line
- Assume that out model is $h_{\theta}(x) = g(\theta_0 + \theta_1 x_1 + \theta_2 x_2)$
- for $\theta = [-3, 1, 1]^T$
- $y = 1$ if $\theta^T x = -3 + x_1 + x_2 \geqslant 0$ (or $x_1 + x_2 \geqslant 3$)
-
- So we have the following decision boundary line
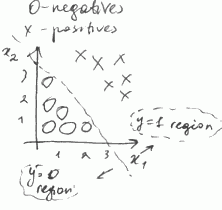
- this line separates two regions: one with “$y = 1$” and another with “$y = 0$”
We may fit as complex expressions as we like
- Suppose we want non-linear decision boundary
-
- we fit polynomial expression:
- $h_{\theta} = g(\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1^2 + \theta_4 x_2^2)$
-
- Assume $\theta = [-1, 0, 0, 1, 1]^T$
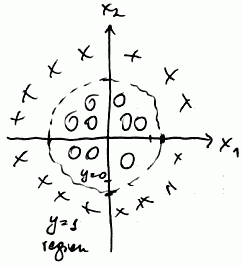
- here we predict “$y = 1$” if $x_1^2 + x_2^2 \geqslant 1$
Examples
Suppose we fit $h_{\theta}(x) = g(\theta_0 + \theta_1 x_1 + \theta_2 x_2)$
-
- with parameters $\theta_0 = -6$, $\theta_1 = 0$ and $\theta_2 = 1$
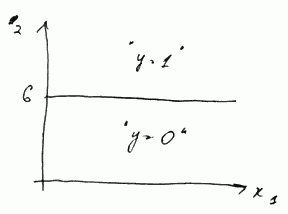
- the transition from negative to positive occur when x_2 goes from below 6 to above 6
-
- if parameters are $\theta_0 = 6$, $\theta_1 = -1$ and $\theta_2 = 0$,
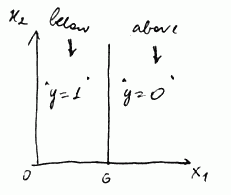
- the transition occurs when $x_1$ goes from above 6 to below 6 (note that $\theta_1 = -1$)
Cost Function
We have:
- Training set ${(x^{(i)}, y^{(i)})}$ with $m$ examples
- each $x = [x_0, …, x_n]^T \in \mathbb{R}^{n + 1}$ where $n$ is a number of features,
- all $x_0 = 1 $
- and all $y \in {0, 1}$
- the model is $h_{\theta} = \cfrac{1}{1 - e^{-\theta^T x}}$
- How to choose parameters $\theta$?
Non-Convex Cost Function
For Linear Regression the cost function was
- $J(\theta) = \cfrac{1}{m} \sum \text{cost}(h_{\theta}(x^{(i)}), y^{(i)})$
- where $\text{cost}(h_{\theta}(x), y) = \cfrac{1}{2} (h_{\theta}(x) - y)^2$
- For logistic regression the problem with this approach is that with the sigmoid function g(z) it gives a non-convex function
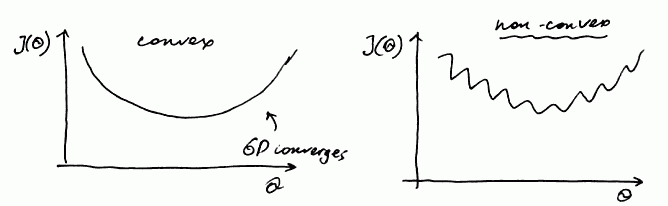
- that is,
- if $J(\theta)$ is non-convex, it has many local optima, and Gradient Descent is not guaranteed to converge to a global optimum
- if $J(\theta)$ is convex, Gradient Descent always converges to a global optimum
- So we need a different cost function that is convex and GD will work on it
Better Cost Function
We can use:
- $\text{cost}(h_{\theta}(x), y) = \left{\begin{array}{l l} -\log(h_{\theta}(x)) & \text{ if } y = 1 \ - \log(1 - h_{\theta}(x)) & \text{ if } y = 0 \end{array} \right. $
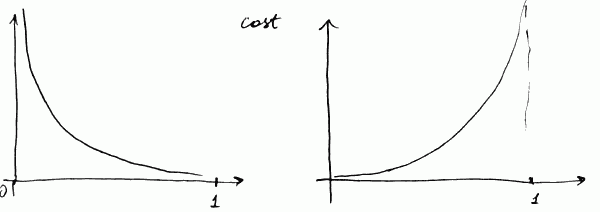
- for the first equation (the left side)
- $\text{cost} = 0$ if $h_{\theta}(x) = 1$ (and $y = 1$)
- as $h_{\theta}(x) \to 0$, $\text{cost} \to \infty$
- it captures the intuition that if $h_{\theta}(x) = 0$, but $y = 1$, we will penalize by a very large cost
- same for the 2nd equation (the right side)
- $\text{cost} \to \infty$ as $h_{\theta}(x) \to 1$
Because $y \in {0, 1}$, we can rewrite the cost function as
- $\text{cost}(h_{\theta}(x), y) = -y \cdot \log(h_{\theta}(x)) - (1 - y) \cdot \log(1 - h_{\theta}(x))$
- and the total cost is $J(\theta) = \cfrac{1}{m} \sum \text{cost}(h_{\theta}(x^{(i)}), y^{(i)}) = - \cfrac{1}{m} \sum \left[ y \cdot \log(h_{\theta}(x)) + (1 - y) \cdot \log(1 - h_{\theta}(x)) \right]$
Fitting $\theta$
- To fit $\theta$ we use Gradient Descent or other optimization technique
- The algorithm is identical to finding $\theta$ for Linear Regression
Basic Algorithm
So the whole Logistic Regression algorithms is:
- find $\min_{\theta} J(\theta)$
- get this $\theta$
- for a new $x$ output $h_{\theta}(x) = g(\theta^T x)$
- using given threshold decide if $y = 1$ or $y = 0$
Additional Notes
Multi-Class Classification
For multi-class classification with Logistic Regression use One-vs-All Classification
Regularization
| To prevent overfitting we reduce magnitude of some features with Regularization
Implementation
Matlab/Octave implementation: