Ontology Based Data Access

Ontology Based Data Access

For querying ontologies

• typically using SPARQL
• keep data in a db (or a triple store), but access it via ontologies
• as a bonus, have inference capabilities during query answering, since it’s based on Logic
• also useful for Data Integration

Query Answering

Difference: Ontologies and traditional Databases

• In DBMS all facts are explicit, but in Semantic Web, there are inferred tuples
• Constraints: can’t violate in RDBMs, additional facts are inferred in SW to satisfy the constraints

Use SPARQL for querying ontologies

• it can be translated to First Order Logic expression and Conjunctive Queries

Example:

SELECT ?x WHERE {
  ?x :EnrolledIn ?y .
  ?z :Leads ?y .
  ?z rdf:type :Professor .
}

Translation:

• FOL: $Q(x) \equiv \forall x \ \exists \ y, z \ : \ \text{EnrolledIn}(x, y) \land \text{Leads}(z, y) \land \text{Professor}(z)$
• CQ: $Q(x) \leftarrow \text{EnrolledIn}(x, y), \text{Leads}(z, y), \text{Professor}(z)$

Inference Approaches

But since the ontologies are backed by some storage,

• need to make sure that inference happens
• otherwise we will just query facts not backed by TBox of our ontology

Main Approaches

'’Cached Inference’’

• inferred triples are stored along with asserted
• risk an explosion of the triple store
• also, change management is important - how to propagate changes and deletes
• for deletes - same inferred tuple can be due to several facts, so need to be careful when deleting

'’Just-In-Time Inference’’

• To respond to queries only
• no inferred triples retained

Compromise

• can be materialization of some inferences tuples

Just-In-Time Inference

Query

• (for ABox and TBox, see Descriptive Logic)
• using both ABox (facts - RDF graph) and TBox (rules - Ontology)
• a triple is in an answer set either
  • because it’s in the ABox
  • or it’s a consequence of some fact from ABox inferred by the TBox

Note:

• FOL $\equiv$ SQL - undecidable for some things we want to have
• so need to have a trade off: CQs (Select-Project-Join Expressions in Relational Algebra)

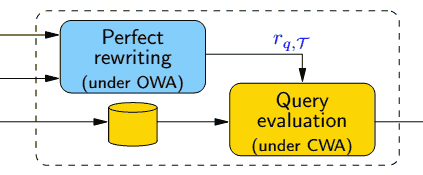
So, Answer set evaluation:

• consists of two phases
• query reformulation (rewriting)
  • translate the original query $q$ into a set of queries $Q$
  • reasoning happens here: Only TBox is accessed
  • algorithm for rewriting: #Perfect Rewriting
• query execution
  • for each $q_i \in { q } \cap Q$
  • execute $q_i$ against the ABox
  • (simply evaluating $q$ will give us an incomplete result)

Example

Consider this query $Q(x)$:

• $Q(x) \leftarrow \text{EnrolledIn}(x, y), \text{Leads}(z, y), \text{Professor}(z)$ can become:

Set of rules (FOL notation)

• $\text{AcademicStaff} (X) \Rightarrow \text{Staff} (X)$
• $\text{Professor}(X) \Rightarrow \text{AcademicStaff} (X)$
• $\text{Lecturer}(X) \Rightarrow \text{AcademicStaff} (X)$
• $\text{PhDStudent}(X) \Rightarrow \text{Lecturer}(X)$
• $\text{PhDStudent}(X) \Rightarrow \text{Student}(X)$
• $\text{TeachesIn}(X, Y) \Rightarrow \text{AcademicStaff}(X)$
• $\text{TeachesIn}(X, Y) \Rightarrow \text{Course}(Y)$
• $\text{ResponsibleOf} (X, Y) \Rightarrow \text{Professor}(X)$
• $\text{ResponsibleOf} (X, Y) \Rightarrow \text{Course}(Y)$
• $\text{TeachesTo}(X, Y) \Rightarrow \text{AcademicStaff} (X)$
• $\text{TeachesTo}(X, Y) \Rightarrow \text{Student}(Y)$
• $\text{Leads}(X, Y) \Rightarrow \text{AdministrativeStaff} (X)$
• $\text{Leads}(X, Y) \Rightarrow \text{Dept}(Y)$
• $\text{RegisteredIn}(X, Y) \Rightarrow \text{Student}(X)$
• $\text{RegisteredIn}(X, Y) \Rightarrow \text{Course}(Y)$
• $\text{ResponsibleOf}(X, Y) \Rightarrow \text{TeachesIn}(X, Y)$
• $\text{Professor}(X) \Rightarrow \exists Y \ : \ \text{TeachesIn}(X, Y)$
• $\text{Course}(X) \Rightarrow \exists Y \ : \ \text{RegisteredIn}(Y, X)$
• $\text{Student}(X) \Rightarrow \lnot \text{Staff} (X)$

The following are reformulations of $Q(x)$

• $q_{1}(x) \leftarrow \text{ResponsibleOf}(x,y), \text{RegisteredIn}(z,y), \text{Student}(z)$
• $q_{2}(x) \leftarrow \text{TeachesIn}(x,y), \text{RegisteredIn}(z,y), \text{PhDStudent}(z)$
• $q_{3}(x) \leftarrow \text{TeachesIn}(x,y), \text{RegisteredIn}(z,y), \text{TeachesTo}(_,z)$
• $q_{4}(x) \leftarrow \text{TeachesIn}(x,y), \text{RegisteredIn}(_,y)$
• $q_{5}(x) \leftarrow \text{ResponsibleOf}(x,y), \text{RegisteredIn}(z,y), \text{PhDStudent}(z) $
• $q_{6}(x) \leftarrow \text{ResponsibleOf}(x,y), \text{RegisteredIn}(z,y), \text{TeachesTo}(_,z)$
• $q_{7}(x) \leftarrow \text{ResponsibleOf}(x,y), \text{RegisteredIn}(_,y)$
• $q_{8}(x) \leftarrow \text{ResponsibleOf}(x,y), \text{RegisteredIn}(z,y), \text{PhDStudent}(z)$
• $q_{9}(x) \leftarrow \text{ResponsibleOf}(x,y), \text{RegisteredIn}(z,y), \text{TeachesTo}(_,z)$
• $q_{10}(x) \leftarrow \text{ResponsibleOf}(x,y), \text{RegisteredIn}(_,y)$
• $q_{11}(x) \leftarrow \text{TeachesIn}(x,y), Course(y)$
• $q_{12}(x) \leftarrow \text{TeachesIn}(x,_)$
• $q_{13}(x) \leftarrow \text{ResponsibleOf}(x,_)$
• $q_{14}(x) \leftarrow \text{Professor}(x)$

And the result is

• union of all queries:
• $q^*(x) \leftarrow q(x) \cup q_1(x) \cup … \cup q_{14}(x)$

Algorithm

Evaluating a query

• given a (Union of) CQs q and DL ontology $O = \langle T, A \rangle$
• compute the perfect rewriting of $q$ over $T$
• evaluate over $A$

Computing the Perfect Rewriting

• start from $q$
• iteratively get $q’$ and collect a union of queries $\text{PR}$
• unify an atom of $q$ using inclusion
• unity an atom on $q’$ to obtain more specific CQ to expand further

Reference:

• Web Data Management book, section 9.4
• “Answering queries through DL-LITE ontologies”
• 9.4.3 Answer set evaluation
• PerfectRef algorithm - page 170

ODBA Architecture

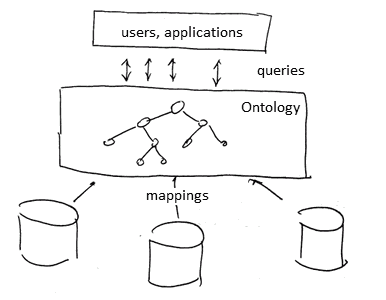
There are 3 main components

• Ontology - unified conceptual view of managed information
• Data Sources - external, possible heterogeneous
• Mappings - map data from DS to ontology

Formalization

A OBDA is $O = \langle T, S, M \rangle$ where

• $T$ - is a DL Tbox
• $S$ - (federated) database that represents the sources
• $M$ - mapping assertions
  • each of the form $\Phi(\vec{x}) \mapsto \Psi(\vec{x})$
  • $\Phi(\vec{x})$ - FOL query over $S$, returns facts - values for $\vec{x}$
  • $\Psi(\vec{x})$ - FOL over $T$
  • so mappings from $M$ translates queries over $S$ to queries over $T$

Mappings

Mappings set $M$

• $M$ is crucial in OBDA
• it encodes how to use data from $S$ to populate elements of $T$

Mappings:

• each mapping $m \in M$ of the form $m: \Phi(\vec{x}) \mapsto \Psi(\vec{x})$
• $\Phi(\vec{x})$ - FOL query over $S$, returns facts - values for $\vec{x}$
• $\Psi(\vec{x})$ - FOL over $T$
• so mappings from $M$ translates queries over $S$ to queries over $T$

Virtual Data Layer (VDL) - virtual ABox

• $S$ and $M$ define a VDL $V = M(S)$
• so, queries are answered using $T$ and $V$
• but we don’t materialize data in $V$ - it’s virtual
• and information in $T$ and $M$ is used to translate queries over $T$ into queries over $S$
• queries over $V$ are answered in the same way:

ODBC in Practice

ONTOP

ONTOP: http://ontop.inf.unibz.it

• implements ODBA for databases in Java as a protege plugin
• Demo Video https://www.youtube.com/watch?v=KHtlARfex4c
• Download: http://ontop.inf.unibz.it/?page_id=179

ONTOP:

• Translates SPARQL to SQL
• Can work as a SPARQL endpoint
• 
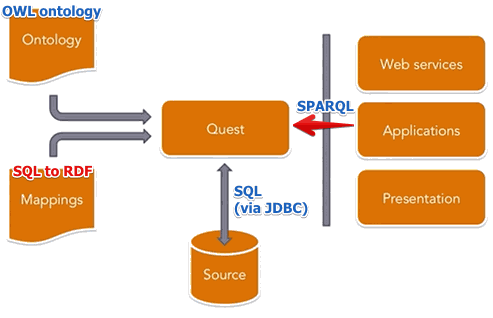
• Quest [http://ontop.inf.unibz.it/?page_id=7] is a component that does the translation

Source

• Web Data Management book [http://webdam.inria.fr/Jorge]
• XML and Web Technologies (UFRT)
• Semantic Web for the Working Ontologist (book)
• Ontology-Based Data Access: From Theory to Practice (presentation) [https://www.inf.unibz.it/~calvanese/presentations/BDA-2012-obda-calvanese.pdf]
• ONTOP Demo Video [https://www.youtube.com/watch?v=KHtlARfex4c]