Partitioned Hash Function Index
Contents
Partitioned Hash Function Index
This is Hash-Based Multi-Dimensional Index Structure
Typical Approach
Suppose we use classical approach for hashing a tuple $(a, b)$
- $h(a, b) = h_1(a) + h_2(b)$
- in this case we need to provide both $a$ and $b$
- but what if we want to query only for $a$?
- this will not work
Partitioned Hash Function
To tackle this problem, we define a hash function $h$ in a different way
- $h(v_1, ..., v_n) = h_1(v_1) || ... || h_n(v_n)$
- where $||$ means concatenation
- so it's a list of functions $h_i$
- $h$ produces $k$-bit output
- each function $h_i$ produces $k_i$ bits and $\sum k_i = k$
Example
- assume we have 1024 buckets, to address each one we need at least 10 bits
- i.e. $k = 10$ and $2^k = 1024$
- suppose we decide (say, based on density, etc) that
- $f(x)$ reserves 2 bits,
- $g(y)$ gets 5 bits and
- $h(z)$ - last 3 bits
-
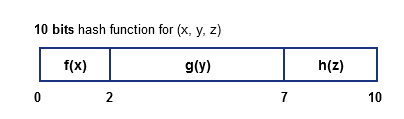
By partition a hash function this way we can query only for some attributes
- suppose we want to query for $x = 10$ and $y = 20$
- calculate hash for there two values
- then we enumerate all possible values for $h(z)$ - and go through them
-
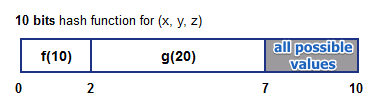
Queries
Good support:
- point queries
- partial match queries
No Support for:
- range queries
- nearest-neighbor queries (physical distance is not reflected in the way we build $h$)
And
- less space wasted than in Grid File Index
See also
Sources
- Database Systems Architecture (ULB)
- Database Systems: The Complete Book (2nd edition) by H. Garcia-Molina, J. D. Ullman, and J. Widom