Positive-Definite Matrices

Positive-Definite Matrices

Energy-Based Definition

In Linear Algebra, a matrix an $n \times n$ matrix is Positive-definite matrix (PDM) if

• $\mathbf v^T A \mathbf v > 0$ for all $\mathbf v \in \mathbb R^n$
• This is the energy based definition

Why ‘‘energy’’?

• because $\mathbf v^T A \mathbf v$ or $\frac{1}{2} \mathbf v^T A \mathbf v$ is called the ‘‘energy’’ of the system $A$

Positive Semi-Definite Matrices

• A matrix is semi-positive definite if
• $\mathbf v^T A \mathbf v \geqslant 0$ for all $\mathbf v \ne \mathbf 0 \in \mathbb R^n$
• so some eigenvectors can be 0

Motivating Example

• Let $A = \begin{bmatrix} 2 & 6
  6 & 18
  \end{bmatrix}$
• then for any $\mathbf x = (x_1, x_2)$ we want to check
• $\big[x_1 \ x_2 \big] \begin{bmatrix} 2 & 6
  6 & 18
  \end{bmatrix} \begin{bmatrix} x_1
  x_2
  \end{bmatrix} = 2 \, x_1^2 + 12 \, x_1 x_2 + 18 \, x_2^2$
• note that this is not a linear anymore:
• we have an equation $a x_1^2 + 2b \, x_1 x_2 + c \, x_2^2$
• this is a Quadratic Form
• we want to know if this quantity is always positive or not
• are there such $x_1, x_2$ that $a x_1^2 + 2b \, x_1 x_2 + c \, x_2^2 < 0$?

So we have a function $f(\mathbf x) = \mathbf x^T A \, \mathbf x$ and we want to check if it’s always positive for any $\mathbf x$

Another example

• let $A_1 = \begin{bmatrix} 2 & 6
  6 & 7
  \end{bmatrix}$
• then $f(\mathbf x) = \mathbf x^T A_1 \, \mathbf x = 2 x_1^2 + 12 x_1 x_2 + 7 x_2^2$
• there exists $\mathbf x$ such that $f(\mathbf x) < 0$, e.g. $(1, -1)$
• in this system, there’s a Saddle Point - a max for one direction and min for another
• 

Consider an alternative:

• $A_2 = \begin{bmatrix} 2 & 6
  6 & 20
  \end{bmatrix}$
• $f(\mathbf x) = \mathbf x^T A_2 \, \mathbf x = 2 x_1^2 + 12 x_1 x_2 + 20 x_2^2$
• here squares always overwhelm $12 x_1 x_2$
• 

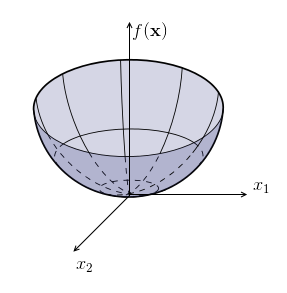
We say that $A_1$ is ‘‘indefinite’’, and $A_2$ is ‘‘positive-definite’’

<img src=”” />

Source: [http://brickisland.net/cs177fa12/?p=302]

Finding Minima

Recall from Calculus:

• 1st Derivative is needed for finding extremum, but you don’t know if it’s min or max
• so you have to look for the 2nd derivative to learn if it’s positive or negative
• you want to find $\cfrac{du}{dx} = 0$ and $\cfrac{d^2 \, u}{d \, x^2} > 0$

Consider $A_2$ again:

• $f(\mathbf x) = \mathbf x^T A_1 \, \mathbf x = 2 x_1^2 + 12 x_1 x_2 + 20 x_2^2$
• Let’s complete the square: $2 \, (x_1 + 3 \, x_2)^2 + 2 \, x_2^2$
• now it’s easy to see that this function is indeed always positive: we completed the square and there are no negative terms

What about $A_1$?

• $f(\mathbf x) = \mathbf x^T A_1 \, \mathbf x = 2 x_1^2 + 12 x_1 x_2 + 7 x_2^2$
• let’s try to complete the square: $2 \, (x_1 + 3 \, x_2)^2 - 11 \, x_2^2$
• we have a minus| | |

  Matrix vs Function

  Let’s have a look again at $A_2$:

• $f(\mathbf x) = \mathbf x^T A_1 \, \mathbf x = 2 x_1^2 + 12 x_1 x_2 + 20 x_2^2 = 2 \, (x_1 + 3 \, x_2)^2 + 2 \, x_2^2$
• the numbers in the completed square form come from Gaussian Elimination| |- Let’s do $A = LU$ transformation: | - $L = \begin{bmatrix} 1 & 0
  3 & 1
  \end{bmatrix}, U = \begin{bmatrix} \boxed 2 & 6
  0 & \boxed 2
  \end{bmatrix}$
• multipliers before squares come from pivots of $U$:
  • $\boxed{2} \, (x_1 + 3 \, x_2)^2 + \boxed 2 \, x_2^2$
• coefficients inside each square come from $L$
  • $2 \, (1 \, x_1 + 3 \, x_2)^2 + 2 \, (0\, x_1 + 1 \, x_2)^2$
• so positive pivots of $U$ are good

Derivative Matrix

So a matrix of second derivatives (Hessian Matrix) is

• $\begin{bmatrix} \cfrac{\partial x_1^2}{\partial^2 x_1} & \cfrac{\partial x_1 \partial x_2}{\partial x_1 \partial x_2}
  \cfrac{\partial x_2 \partial x_1}{\partial x_2 \partial x_1} & \cfrac{\partial x_2^2}{\partial^2 x_2}
  \end{bmatrix}$
• we want it to be positive-definite
• then the function $f(\mathbf x) = \mathbf x^T A \, \mathbf x$ is positive-definite

Checking for Positiveness

So, how to check for positive definitiveness?

• using the definition: check that $\mathbf v^T A \mathbf v > 0$ for all $\mathbf v$
• check that all eigenvalues are positive
• or that all pivots of $L$ in $A = LU$ are positive
• or that all Determinants and sub-determinants are positive

Checking using positiveness of eigenvalues:

• if for all $\mathbf v$, $\mathbf v^T A \, \mathbf v > 0$,
• $A \mathbf v = \lambda \mathbf v$, multiply by $\mathbf v^T$ on the left
• $\mathbf v^T A \, \mathbf v = \lambda \mathbf v^T \mathbf v$

• $\mathbf v^T A \, \mathbf v = \lambda | \mathbf v |^2$

  - $| \mathbf v |^2$ is always positive, so it means that if $\lambda > 0$, then so is $\mathbf v^T A \, \mathbf v$

  - therefore we can check if all eigenvalues are positive

Properties

Sum

If $A$ and $B$ are both PDM

• then so is $A + B$
• because the energies add when we add matrices:
• $\mathbf v^T A \, \mathbf v + \mathbf v^T B \, \mathbf v$

Inverse

• if $A$ is PDM, the inverse is also PDM
• eigenvalues of the inverse are $\lambda^*_i = \frac{1}{\lambda_i}$
• so eigenvalues are also positive

• but careful with semi-positive definite matrices: they do not have an inverse

$R^T R$ and $R R^T$ Matrices

They are always semi-positive definite

• see Gram Matrices

Sources

• Linear Algebra MIT 18.06 (OCW)
• Jauregui, Jeff. “Principal component analysis with linear algebra.” (2012). [http://www.math.union.edu/~jaureguj/PCA.pdf]