Determinants
A ‘‘determinant’’ is a value associated with a square matrix $A$
- it provides important information about invertability of the matrix
-
it’s denoted as $\text{det } A$ or sometimes $ A $
Defining Properties
These properties define what a determinant is (they don’t say how to compute it)
Property 1: Determinant of $I$
- $\text{det } I = 1$
Property 2: Sign Reversal
- let $A’$ be a matrix $A$ with two rows exchanged, then $\text{det } A’ = \text{det } A$
Consequence of property 2:
- for a Permutation Matrix $P$
- $\text{det } P = 1$ if if has even number of row exchanges
- and $\text{det } P = -1$ is it has odd number of exchanges
Property 3: Linearity
- determinant is a linear function of a row - if all other rows stays the same
- 3a) $\begin{vmatrix} t a_{11} & t a_{12} & t a_{13} \ a_{21} & a_{22} & a_{23} \ a_{31} & a_{32} & a_{33} \ \end{vmatrix} = t \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \ a_{21} & a_{22} & a_{23} \ a_{31} & a_{32} & a_{33} \ \end{vmatrix}$
- 3b) $\begin{vmatrix} a_{11} + a’{11} & a{12} + a’{12} & a{13} + a’{13} \ a{21} & a_{22} & a_{23} \ a_{31} & a_{32} & a_{33} \ \end{vmatrix} = \begin{vmatrix} a_{11} & a_{12} & a_{13} \ a_{21} & a_{22} & a_{23} \ a_{31} & a_{32} & a_{33} \ \end{vmatrix} + \begin{vmatrix} a’{11} & a’{12} & a’{13} \ a{21} & a_{22} & a_{23} \ a_{31} & a_{32} & a_{33} \ \end{vmatrix}$
- applies to all the rows: we always can put any row to the first position (property 2), then apply the property 3, and then put the row back
Other properties
These properties are consequences of the defining properties
Property 4: Equal Rows
- if 2 rows are equal, then $\text{det } A = 0$
- proof: if we exchange two rows, nothing happens to the matrix, but property 2 says the sign should be reversed
Property 5: Linear Combinations
- if we subtract a multiple of row $i$ from the row $k$, the determinant remains the same
- for Gaussian Elimination it means that $\text{det } A = \text{det } U$
- $\begin{vmatrix}
a_{11} & a_{12} \
a_{21} - c a_{11} & a_{22} - c a_{12} \
\end{vmatrix} \ \mathop{=}\limits^{3^{\circ}}
\begin{vmatrix} a_{11} & a_{12} \ a_{21} & a_{22} \ \end{vmatrix} - c \begin{vmatrix} a_{11} & a_{12} \ a_{11} & a_{12} \ \end{vmatrix} \ \mathop{=}\limits^{4^{\circ}}
\begin{vmatrix} a_{11} & a_{12} \ a_{21} & a_{22} \ \end{vmatrix} - c 0 = \begin{vmatrix} a_{11} & a_{12} \ a_{21} & a_{22} \ \end{vmatrix}$
Property 6: Zero Row
- if we have a rows full of zeros, then $\text{det } A = 0$
- $c \cdot \begin{vmatrix} a_{11} & a_{12} \ 0 & 0 \ \end{vmatrix} = \begin{vmatrix} a_{11} & a_{12} \ c \cdot 0 & c \cdot 0 \ \end{vmatrix} = \begin{vmatrix} a_{11} & a_{12} \ 0 & 0 \ \end{vmatrix}$
- the only possible way for this to be valid is when the det is 0
Property 7: Determinant of $U$
- for upper-triangular matrix $U$, determinant of $U$ is the product of elements on the main diagonal
- $\begin{vmatrix} d_1 & 0 & 0 \ a_{21} & d_2 & 0 \ a_{31} & a_{32} & d_3 \ \end{vmatrix} = \prod d_i$
Why?
- if we can do $LU$ factorization, then we can do $LDU$ factorization as well
- and by property 5, $\text{det } A = \text{det } U = \text{det } D$
- $\begin{vmatrix} d_1 & 0 & 0 \ 0 & d_2 & 0 \ 0 & 0 & d_3 \ \end{vmatrix} \ \mathop{=}\limits^{3^{\circ}} \ d_1 \cdot \begin{vmatrix} 1 & 0 & 0 \ 0 & d_2 & 0 \ 0 & 0 & d_3 \ \end{vmatrix} = d_1 d_2 \cdot \begin{vmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & d_3 \ \end{vmatrix} = d_1 d_2 d_3 \cdot \text{det } I = \prod d_i$
Consequence:
- the easiest way to compute the determinant is to apply $A = LU$ Factorization and then compute $\text{det } U = \prod_i d_i$
-
note that you should be careful with row exchanges - what if some $d_i = 0$? then $\text{det } U = 0$
-
Property 8: Singularity Test
- when $A$ is singular, then $\text{det } A = 0$
- when $A$ is non-singular, then $\text{det } A \ne 0$
- it makes it a good test for invertability
Why?
- directly follows from property 7
- compute $A = LU$ factorization
- if the matrix is singular, then at least one $d_i = 0$, then $\text{det } U = 0$
- if $A$ is not singular, then no pivot is 0, thus $\text{det } U \ne 0$
Property 9: Product Rule
- $\text{det } AB = \text{det } A \cdot \text{det } B$
Proof:
- consider ratio $D(A) = \cfrac{\text{det } AB}{\text{det } B}$ (for $\text{det } B \ne 0$)
- note that $D(A)$ obeys the properties 1, 2, 3 of $\text{det } A$
- property 1: if $A = I$, then $D(A) = \cfrac{\text{det } IB}{\text{det } B} = 1$
- property 2: if we exchange two rows of $A$, the same rows are exchanged for $AB$, thus $\text{det } AB$ changes the sign, and so does $D(A)$
- property 3:
- 3a) multiply row 1 of $A$ by $c$, then row 1 of $AB$ also gets multiplied by $c$
- 3b) add $[a’{11}, \ … \ , a’{1n}]$ to row 1 of $A$ - then row 1 of $AB$ gets row 1 of $A’ B$ (where $A’$ is $A$ with row 1 replaced)
- illustration: $\text{det } \begin{bmatrix} a_{11} + a’{11} & a{12} + a’{12} \ … & … \ \end{bmatrix} \begin{bmatrix} b{11} & b_{12} \ b_{21} & b_{22} \ \end{bmatrix} = $ $\begin{vmatrix} (a_{11} + a’{11}) b{11} + (a_{12} + a’{12}) b{21} & (a_{11} + a’{11}) b{12} + (a_{12} + a’{12}) b{22}\ … & … \ \end{vmatrix} = $ $\begin{vmatrix} a_{11} b_{11} + a_{12} b_{21} & a_{11} b_{12} + a_{12} b_{22}\ … & … \ \end{vmatrix} +$ $\begin{vmatrix} a’{11} b{11} + a’{12} b{21} & a’{11} b{12} + a’{12} b{22}\ … & … \ \end{vmatrix}$
- thus $D(A)$ obeys the same properties as $\text{det } A$, so $D(A) = \text{det } A$ and we have $\text{det } AB = \text{det } A \cdot \text{det } B$
Consequence:
- $I = A^{-1} A$
- $\text{det }I = \text{det }A^{-1} A$
- $\text{det }A^{-1} \cdot \text{det } A = 1$
- $\text{det }A^{-1} = \cfrac{1}{\text{det } A}$
Consequence 2:
- now can take into account the permutation matrix $P$ in the $PA = LU$ decomposition
- $\text{det } PA = \text{det } LU$
- $\text{det } P \cdot \text{det } A = \text{det } L \cdot \text{det } U$
- $\text{det } P = \pm 1$, $\text{det } L = 1$ (elements on the diagonal of $L$ are 1’s)
- so $\text{det } A = \text{det } P \cdot \text{det } U$
Property 10: Transposition
$\text{det } A^T = \text{det } A$
- The transpose of $A$ has the same determinant as $A$
Proof:
- consider $PA = LU$ factorization
- transpose: $A^T P^T = U^T L^T$
- take determinant, apply property 10 and compare $\text{det }P \cdot \text{det }A = \text{det } L \cdot \text{det } U$ with $\text{det }A^T \cdot \text{det }P^T = \text{det }U^T \cdot \text{det } L^T$
- $\text{det } L = \text{det } L^T = 1$ (both have 1’s on the diagonal)
- $\text{det } U = \text{det } U^T = \prod d_i$ - they have the same elements on the diagonal
- finally $\text{det } P = \text{det } P^T$ because $P^T P = I$ ($P$ is orthogonal) and by property 9 have $\text{det } P^T \cdot \text{det } P = 1$. That happens only when they agree on the sign.
- thus, $\text{det } A^T = \text{det } A$
Consequence
- all the properties above are applied to rows, but the property #10 says that we can apply them to columns as well
Calculating Determinants
There are several possible ways to calculate determinants:
- the Determinant Formula
- the Pivot Formula
- Cofactors
Determinant Formula
Let’s try to find out how we can compute the determinant using the properties
$2 \times 2$ case
- $\begin{vmatrix} a_{11} & a_{12} \ a_{21} & a_{22} \ \end{vmatrix} = \ …$
- can use the property 3 to divide the problem into smaller parts, and solve them separately
- $… \ = \begin{vmatrix}
a_{11} + 0 & 0 + a_{12} \
a_{21} & a_{22} \
\end{vmatrix}
\ \mathop{=}\limits^{3^{\circ}}
\begin{vmatrix} a_{11} & 0 \ a_{21} & a_{22} \ \end{vmatrix} + \begin{vmatrix} 0 & a_{12} \ a_{21} & a_{22} \ \end{vmatrix} = \underbrace{\begin{vmatrix} a_{11} & 0 \ a_{21} & 0 \ \end{vmatrix}}{0} + \begin{vmatrix} a{11} & 0 \ 0 & a_{22} \ \end{vmatrix} + \begin{vmatrix} 0 & a_{12} \ a_{21} & 0 \ \end{vmatrix} + \underbrace{\begin{vmatrix} 0 & a_{12} \ 0 & a_{22} \ \end{vmatrix}}_{0} = \ …$ - by property 6 (zero row) and 10 (determinant of transpose), we know that some parts are 0. so we’re left with
- $… \ = \begin{vmatrix} a_{11} & 0 \ 0 & a_{22} \ \end{vmatrix} + \begin{vmatrix} 0 & a_{12} \ a_{21} & 0 \ \end{vmatrix} = \ …$
- now can change the rows of the second summand by property 2 (sign reversal) and get
- $… \ = \begin{vmatrix} a_{11} & 0 \ 0 & a_{22} \ \end{vmatrix} - \begin{vmatrix} a_{21} & 0 \ 0 & a_{12} \ \end{vmatrix} = a_{11}a_{22} - a_{21}a_{12}$
$3 \times 3$ case
Can do the same for $3 \times 3$ matrices
- $\begin{vmatrix}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23}
a_{31} & a_{32} & a_{33}
\end{vmatrix} = \ …$ - we follow the same divide and conquer approach
- most of the terms will go away because they will be equal to 0
- the “survivers” will have one non-zero entry from each row
- so for $3 \times 3$ we have:
- $… \ = \begin{vmatrix}
a_{11} & 0 & 0\
0 & a_{22} & 0
0 & 0 & a_{33}
\end{vmatrix} + \begin{vmatrix} a_{11} & 0 & 0\ 0 & 0 & a_{23}
0 & a_{32} & 0
\end{vmatrix} + \begin{vmatrix} 0 & a_{12} & 0\ a_{21} & 0 & 0
0 & 0 & a_{33}
\end{vmatrix} + \begin{vmatrix} 0 & a_{12} & 0\ 0 & 0 & a_{23}
a_{31} & 0 & 0
\end{vmatrix} + \begin{vmatrix} 0 & 0 & a_{13}\ a_{21} & 0 & 0
0 & a_{32} & 0
\end{vmatrix} + \begin{vmatrix} 0 & 0 & a_{13}\ 0 & a_{22} & 0
a_{31} & 0 & 0
\end{vmatrix}$ - let’s have a closer look at each of them
- $\begin{vmatrix}
a_{11} & 0 & 0\
0 & a_{22} & 0
0 & 0 & a_{33}
\end{vmatrix} = a_{11}a_{22}a_{33}$, diagonal and nice - $\begin{vmatrix}
a_{11} & 0 & 0\
0 & 0 & a_{23}
0 & a_{32} & 0
\end{vmatrix} = - a_{11}a_{23}a_{32}$ - need 1 row exchange to transform it to $I$-like form - $\begin{vmatrix}
0 & a_{12} & 0\
a_{21} & 0 & 0
0 & 0 & a_{33}
\end{vmatrix} = - a_{12}a_{21}a_{33}$ - also 1 flip away - $\begin{vmatrix}
0 & a_{12} & 0\
0 & 0 & a_{23}
a_{31} & 0 & 0
\end{vmatrix} = a_{12}a_{23}a_{31}$ - 2 exchanges, - $\begin{vmatrix}
0 & 0 & a_{13}\
a_{21} & 0 & 0
0 & a_{32} & 0
\end{vmatrix} = a_{13}a_{21}a_{32}$ - 2 exchanges - $\begin{vmatrix}
0 & 0 & a_{13}\
0 & a_{22} & 0
a_{31} & 0 & 0
\end{vmatrix} = -a_{13}a_{22}a_{31}$ - 3 exchanges
- $\begin{vmatrix}
a_{11} & 0 & 0\
0 & a_{22} & 0
So, the formula for $3 \times 3$:
- $\begin{vmatrix}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23}
a_{31} & a_{32} & a_{33}
\end{vmatrix} = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} - a_{13}a_{22}a_{31}$ - or, schematically:
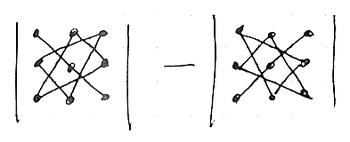
$n \times n$ case: “Big Formula”
The big formula:
-
we consider all $n $ possible permutation matrices $P$ - why $n $? we can choose an element from the row 1 in $n$ ways, an element from the row 2 in $n - 1$ ways, …, the last - in one way - $\text{det } A = \sum\limits_{\text{$n $ permutations $P$}} \text{det } P \cdot a_{1\alpha_1} a_{2\alpha_2} … a_{n\alpha_n}$ - where $\boldsymbol \alpha = (\alpha_1, \ … \ , \alpha_n)$ is a Permutation of $(1, \ … \ , n)$
The Pivot Formula
The easiest way is to use the properties 2, 5, 7 and 9:
- do the factorization $PA = LU$
- know that $\text{det } A = \text{det } P \cdot \text{det } U$
- if one of the pivots is 0, then $\text{det } A = 0$
- if $P$ is $\pm 1$, depending on the number of permutations, and $\text{det } U = \prod d_i$
Cofactors
Cofactors give a way to break $n \times n$ determinant to $(n - 1) \times (n - 1)$ determinants
$3 \times 3$ Case: Intuition
Suppose $A$ is a $3 \times 3$ matrix
- $\begin{vmatrix}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23}
a_{31} & a_{32} & a_{33}
\end{vmatrix} = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} - a_{13}a_{22}a_{31}$ - let’s group them
- $\text{det } A = a_{11} (a_{22}a_{33} - a_{23}a_{32}) + a_{12} (-1) (a_{21}a_{33} - a_{23} a_{33}) + a_{13} (a_{21}a_{32} - a_{22}a_{31})$
- note that now in parentheses we have determinants of smaller matrices| | - for $a_{11}$ we have $a_{22}a_{33} - a_{23}a_{32} = \begin{vmatrix} |a_{22} & a_{23}
a_{32} & a_{33}
\end{vmatrix}$- for $a_{12}$ we have $- (a_{21}a_{33} - a_{23} a_{33}) = - \begin{vmatrix}
a_{21} & a_{23}
a_{31} & a_{33}
\end{vmatrix}$ (note the $-$ sign| ) | - for $a_{13}$ we have $a_{21}a_{32} - a_{22}a_{31} = \begin{vmatrix} |a_{21} & a_{22}
a_{31} & a_{32}
\end{vmatrix}$ - these are co-factors of $a_{11}, a_{12}, a_{13}$ respectively
- for $a_{12}$ we have $- (a_{21}a_{33} - a_{23} a_{33}) = - \begin{vmatrix}
a_{21} & a_{23}
- so we can write this as
- $\begin{vmatrix}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23}
a_{31} & a_{32} & a_{33}
\end{vmatrix} = \begin{vmatrix} a_{11} & 0 & 0\ 0 & a_{22} & a_{23}
0 & a_{32} & a_{33}
\end{vmatrix} - \begin{vmatrix} 0 & a_{12} & 0\ a_{21} & 0 & a_{23}
a_{31} & 0 & a_{33}
\end{vmatrix} + \begin{vmatrix} 0 & 0 & a_{13}\ a_{21} & a_{22} & 0
a_{31} & a_{32} & 0
\end{vmatrix}$
- $\begin{vmatrix}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23}
Cofactors
a ‘‘cofactor’’ of $a_{ij}$ is $C_{ij}$
- $C_{ij}$ is a determinant of a $n - 1$ matrix - it’s a matrix $A$ with row $i$ and column $j$ removed
- note that we can have a minus sign before some of the cofactors
- we have $C_{ij}$ with $-$ if $i+j$ is odd, and $+$ if $i+j$ is even
- so for $3 \times 3$ matrix we take signs this way: $\begin{vmatrix}
- & - & + \
- & + & - \
- & - & +
\end{vmatrix}$
a ‘‘minor’’ of $a_{ij}$ is $M_{ij}$
- it’s the same as cofactor, but always with the same sign
The Cofactor Formula
We can take co-factors along any row or column
- suppose we take it along row 1
- then the formula is $\text{det } A = a_{11} C_{11} + a_{12} C_{12} + \ … \ + a_{1n} C_{1n}$
Applications
What can we do with determinants?
Cramer’s Rule
through the Cramer’s Rule:
- Find the inverse and solve a System of Linear Equations
Volume
$\text{det } A$ = volume of a parallelepiped formed by vector-rows of $A$
- $A = \begin{bmatrix}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23}
a_{31} & a_{32} & a_{33}
\end{bmatrix}$ - $\mathbf r_1 = \Big[a_{11} \ \ a_{12} \ \ a_{13} \Big]$
- $\mathbf r_2 = \Big[a_{21} \ \ a_{22} \ \ a_{23} \Big]$
- $\mathbf r_3 = \Big[a_{31} \ \ a_{32} \ \ a_{33} \Big]$

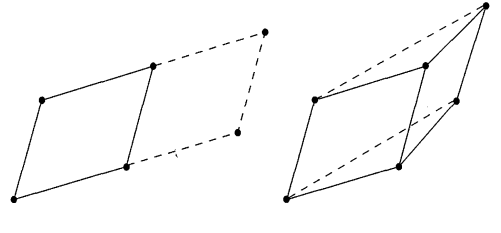
$| \text{det } A|$ is the volume of the box formed by vectors $\mathbf r_1, \mathbf r_2, \mathbf r_3$ | To check if this is indeed true, we need to verify that the volume obeys the 3 defining properties
- $A = I$ works, the volume is 1
- property 2: reversing two rows changes the sign (don’t care), but the volume remains the same - true
- linearity:
- 3a. suppose we double one edge: the volume double
- 3b. see pictorially
Area of Triangle
We know how to compute the area of a square
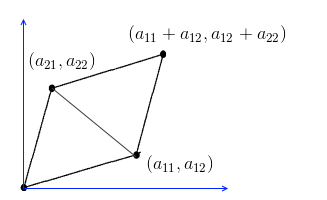
- so we can compute the area of a triangle| |- let $A$ be $2 \times 2$ matrix, $A = \begin{bmatrix} |a_{11} & a_{12} \
a_{21} & a_{22}
\end{bmatrix}$ - the area of a triangle that starts in origin is $\cfrac{1}{2} \text{det } A = \cfrac{1}{2} (a_{11} \, a_{22} - a_{12} \, a_{21}) $
What is it doesn’t start in origin?

- then we calculate it by taking the following determinant:
- $\begin{vmatrix}
x_1 & y_1 & 1 \
x_1 & y_1 & 1
x_1 & y_1 & 1
\end{vmatrix}$
Sources
- Linear Algebra MIT 18.06 (OCW)
- Strang, G. Introduction to linear algebra.
- Курош А.Г. Курс Высшей Алгебры