Reachability Graph
This is a way of representing the states of Petri Nets
A marking $M$ is reachable from the initial marking $M_0$
- $\iff M_0 \to^* M$
- i.e. there exists a firing sequence that brings us from the initial state of a petri net to a state that corresponds to $M_0$
In a ‘‘reachability graph’’ of a petri net $N = (P, T, F)$
- nodes correspond to reachable markings
- edges correspond to the relation $\to$
There can be several notations for markings:
- first one: $(n_1, n_2, …, n_m)$ corresponds to the number of elements in the places $(p_1, …, p_m)$ respectively
- second one: $[p_1^{n_1}, …, p_m^{n_m}]$ where $n_i$ is the number of times $p_i$ appears
- if $p_i$ appears zero times, we don’t show it in the marking
Consider this example:

- so a reachability graph shows all possible states (markings) that you can reach by triggering transitions that are enabled

- the graph above is the reachability graph with different notation
There are some desirable properties for the Workflow Nets
- we want to be able to decide on them
- reachability graphs can be used for that
Coverability Graph
This is a similar notion for expressing states of Workflow Nets
- but unlike Reachability Graph it can be finite for unbounded nets
- yet in many cases less expressive
Examples
Example 1
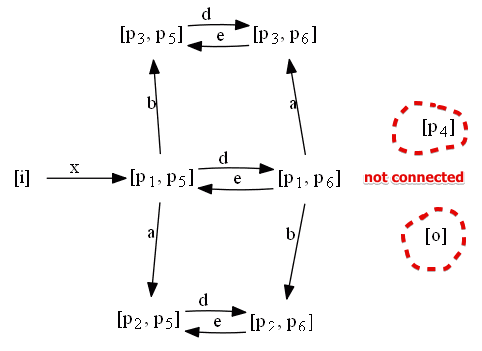
- it is a reachability graph for
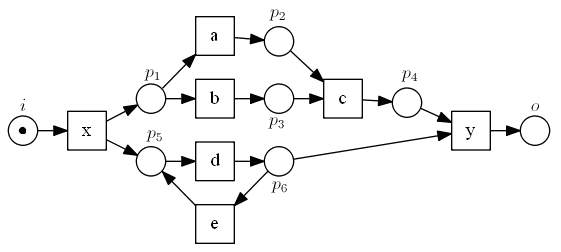
- we see that two nodes are not connected: it’s clearly a problem