$\require{color}$
Sequence Mining
Data Model
- similar to Local Pattern Discovery
- item - binary-valued attribute (either present - 1, or not present - 0)
- itemset - lexicographically sorted subset of all items
- sequence - an ordered list of itemsets (i.e. transactions)
- they may be ordered by date/time, location, price, etc
Sequence Data
Examples
Supermarket
- a supermarket: each product is an item
- A receipt - an itemset (don’t consider the quantity)
- for a certain customer, all his receipt ordered by date form a sequence of transactions
Web:
- each user session is a sequence
- each click is an itemset
- items: remote hosts, user names, date, URLs, etc
NLP:
- text - sequence with Part of Speech Tagging
- sentence - itemset
- words with POS-tags - items
Notation
- items: lowercase letters $a,b,c,…$
- itemsets: uppercase letters $I=(abc), I’=(abc), I_1=(abc)$
- sequence:
- $s = \langle I_1 \ I_2 \ … \ I_k \rangle$ or
- $s = \langle (ab)(c)(bdc) \rangle \equiv \langle (ab)c(bdc) \rangle$
- note that $\langle abc \rangle \equiv \langle (a)(b)(c) \rangle \not \equiv \langle (abc) \rangle$
Subsequences
Sequence containment:
- $s$ is contained in $s’$ ($s \sqsubseteq s’$) $\iff$
- $\forall I \in s$ (in order) $\exists I’ \in s’$ (in order) s.t. $I \subseteq I’$
-
order is important - $s’$ is a super sequence for $s$, or $s’$ “supports” $s$
Example:
- $\langle (a)(bc)(d)(c) \rangle \sqsubseteq \langle (a)(abc)(ac)(d)(cf) \rangle$
- $\langle (a)(b)(cd)(c) \rangle \not \sqsubseteq \langle (a)(abc)(ac)(d)(cf) \rangle$

Sequential Pattern Mining
Like in Local Pattern Discovery, we have the notion of Support
- the support of sequence $s$ w.r.t to dataset $D$ is the # of sequenced in $D$ that support $s$
- $\text{supp}(s, D) = \big| { s’ \in D \ : \ s \sqsubseteq s’ } \big|$ | Frequent patterns:
- a sequence $s$ is frequent if $\text{supp}(s, D) \geqslant \theta$
- where $\theta$ is the desired minimal support (parameter)
- A frequent (sub)sequence is called a ‘‘sequential pattern’’
Sequential Pattern Mining
- given a sequence database $D$, find the complete set of all frequent subsequences
Example
Given:
- Support threshold $\theta = 3$
- Database $D$
| SID | Sequence | 10 | $\langle (a)(abc)(ac)(d)(af) \rangle$ | 20 | $\langle (ad)(c)(bc)(ae) \rangle$ | 30 | $\langle (ef)(ab)(df)(c)(b) \rangle$ | 40 | $\langle (ae)(af)(c)(b)(cf) \rangle$ | 50 | $\langle (abd)(af)(c)(b)(ad) \rangle$ |
Which of the following patterns are frequent?
- $\langle (a) \rangle$
- $\langle (a)(bc) \rangle$
- $\langle (a)(b)(c) \rangle$
- $\langle (a)(b)(c)(d) \rangle$
| Pattern | Frequency | Table | $\langle (a) \rangle$ | 5 | $\langle (\colorbox{red}{a})(abc)(ac)(d)(af) \rangle$ $\langle (\colorbox{red}{a}d)(c)(bc)(ae) \rangle$ $\langle (ef)(\colorbox{red}{a}b)(df)(c)(b) \rangle$ $\langle (\colorbox{red}{a}e)(af)(c)(b)(cf) \rangle$ $\langle (\colorbox{red}{a}bd)(af)(c)(b)(ad) \rangle$ |
$\langle (a)(bc) \rangle$ | 2 | $\langle (\colorbox{red}{a})(\colorbox{red}{ab}c)(ac)(d)(af) \rangle$ $\langle (\colorbox{red}{a}d)(c)(\colorbox{red}{bc})(ae) \rangle$ $\langle (ef)(ab)(df)(c)(b) \rangle$ $\langle (ae)(af)(c)(b)(cf) \rangle$ $\langle (abd)(af)(c)(b)(ad) \rangle$ |
$\langle (a)(b)(c) \rangle$ | 2 | $\langle (\colorbox{red}{a})(a\colorbox{red}{b}c)(a\colorbox{red}{c})(d)(af) \rangle$ $\langle (ad)(c)(bc)(ae) \rangle$ $\langle (ef)(ab)(df)(c)(b) \rangle$ $\langle (\colorbox{red}{a}e)(af)(c)(\colorbox{red}{b})(\colorbox{red}{c}f) \rangle$ $\langle (abd)(af)(c)(b)(ad) \rangle$ |
$\langle (a)(b)(c)(d) \rangle$ | 1 | $\langle (\colorbox{red}{a})(a\colorbox{red}{b}c)(a\colorbox{red}{c})(\colorbox{red}{d})(af) \rangle$ $\langle (ad)(c)(bc)(ae) \rangle$ $\langle (ef)(ab)(df)(c)(b) \rangle$ $\langle (ae)(af)(c)(b)(cf) \rangle$ $\langle (abd)(af)(c)(b)(ad) \rangle$ |
Downwards Closure
Frequency is an anti-monotonic property of a Lattice
- it’s sometimes called “Apriori Property”
- it forms the down-wards closure
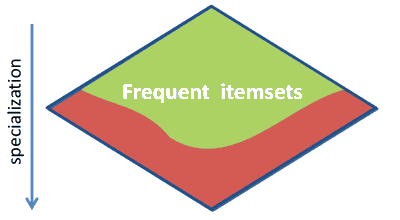
Downwards Closure property
- if a sequence is frequent, then all its subsequences are frequent
E.g.
- if $\langle (a)(bc) \rangle$ is frequent, then
- $\langle (a) \rangle$, $\langle (b) \rangle$, $\langle (c) \rangle$, $\langle (bc) \rangle$, $\langle (a)(b) \rangle$, and $\langle (a)(c) \rangle$ are also frequent
Sequential Apriori Approach
Can adapt Apriori to mining sequential patterns:
- R. Agrawal and R. Srikant. Mining sequential patterns. 1995.
Algorithm
Sequential Apriori
- at level 1
- generate length-1 sequences: ones that contain only 1 itemset of 1 item
- prune non-frequent
- at level $i$
- generate length-$i$ candidate sequences from frequent length-$(i-1)$ sequences
- prune non-frequent
Example
Given
- items $a, b, c, d, e, f, g, h$
- the following database $D$
\langle (a) \rangle, \langle (b) \rangle, \langle (c) \rangle, \langle (d) \rangle, \langle (e) \rangle, \langle (f) \rangle, \langle (g) \rangle, \langle (h) \rangle
| SID | Sequence | 10 | $\langle (bd)(c)(b)(ac) \rangle$ | 20 | $\langle (bf)(ce)(b)(fg) \rangle$ | 30 | $\langle (ah)(bf)(a)(b)(f) \rangle$ | 40 | $\langle (be)(ce)(d) \rangle$ | 50 | $\langle (a)(bd)(b)(c)(b)(ade) \rangle$ |
’'’Step 1:’’’
- generate length-1 candidates
- $\langle (a) \rangle, \langle (b) \rangle, \langle (c) \rangle, \langle (d) \rangle, \langle (e) \rangle, \langle (f) \rangle, \langle (g) \rangle, \langle (h) \rangle$
- calculate frequency
- $\text{freq}\big(\langle (a) \rangle \big) = 3$
- $\text{freq}\big(\langle (b) \rangle \big) = 5$
- $\text{freq}\big(\langle (c) \rangle \big) = 4$
- $\text{freq}\big(\langle (d) \rangle \big) = 3$
- $\text{freq}\big(\langle (e) \rangle \big) = 3$
- $\text{freq}\big(\langle (f) \rangle \big) = 2$
- $\text{freq}\big(\langle (g) \rangle \big) = {\color{red}{1}}$
- $\text{freq}\big(\langle (h) \rangle \big) = {\color{red}{1}}$
- prune non-frequent: $\langle (g) \rangle$ and $\langle (h) \rangle$
’'’Step 2’’’ Now need to generate length-2 candidates
- two ways
- adding an item to a new itemset, i.e. $\langle (a) \rangle$ becomes $\langle (a)(b) \rangle$ when we add $b$
- adding to last itemset: $\langle (a) \rangle$ becomes $\langle (ab) \rangle$
So we have the following candidates:
| | + Way 1 || | $\langle (a) \rangle$ | $\langle (b) \rangle$ | $\langle (c) \rangle$ | $\langle (d) \rangle$ | $\langle (e) \rangle$ | $\langle (f) \rangle$ | $\langle (a) \rangle$ | $\langle (a)(a) \rangle$ | $\langle (a)(b) \rangle$ | $\langle (a)(c) \rangle$ | $\langle (a)(d) \rangle$ | $\langle (a)(e) \rangle$ | $\langle (a)(f) \rangle$ || $\langle (b) \rangle$ | $\langle (b)(a) \rangle$ | $\langle (b)(b) \rangle$ | $\langle (b)(c) \rangle$ | $\langle (b)(d) \rangle$ | $\langle (b)(e) \rangle$ | $\langle (b)(f) \rangle$ || $\langle (c) \rangle$ | $\langle (c)(a) \rangle$ | $\langle (c)(b) \rangle$ | $\langle (c)(c) \rangle$ | $\langle (c)(d) \rangle$ | $\langle (c)(e) \rangle$ | $\langle (c)(f) \rangle$ || $\langle (d) \rangle$ | $\langle (d)(a) \rangle$ | $\langle (d)(b) \rangle$ | $\langle (d)(c) \rangle$ | $\langle (d)(d) \rangle$ | $\langle (d)(e) \rangle$ | $\langle (d)(f) \rangle$ || $\langle (e) \rangle$ | $\langle (e)(a) \rangle$ | $\langle (e)(b) \rangle$ | $\langle (e)(c) \rangle$ | $\langle (e)(d) \rangle$ | $\langle (e)(e) \rangle$ | $\langle (e)(f) \rangle$ || $\langle (f) \rangle$ | $\langle (f)(a) \rangle$ | $\langle (f)(b) \rangle$ | $\langle (f)(c) \rangle$ | $\langle (f)(d) \rangle$ | $\langle (f)(e) \rangle$ | $\langle (f)(f) \rangle$ | | | + Way 2 || | $\langle (a) \rangle$ | $\langle (b) \rangle$ | $\langle (c) \rangle$ | $\langle (d) \rangle$ | $\langle (e) \rangle$ | $\langle (f) \rangle$ | $\langle (a) \rangle$ | | $\langle (ab) \rangle$ | $\langle (ac) \rangle$ | $\langle (ad) \rangle$ | $\langle (ae) \rangle$ | $\langle (af) \rangle$ || $\langle (b) \rangle$ | | | $\langle (bc) \rangle$ | $\langle (bd) \rangle$ | $\langle (be) \rangle$ | $\langle (bf) \rangle$ || $\langle (c) \rangle$ | | | | $\langle (cd) \rangle$ | $\langle (ce) \rangle$ | $\langle (cf) \rangle$ || $\langle (d) \rangle$ | | | | | $\langle (de) \rangle$ | $\langle (df) \rangle$ || $\langle (e) \rangle$ | | | | | | $\langle (ef) \rangle$ || $\langle (f) \rangle$ | | | | | | | |
Now we prune infrequent
And so on…
Drawbacks
- Exponential growth in # of combinations
- Computationally expensive
PrefixSpan
PrefixSpan: A prefix-projected pattern growth method
- Pei et al. PrefixSpan: Mining sequential patterns efficiently by prefix-projected pattern growth, 2001.
- doesn’t generate non-existing patterns (like Apriori)
Idea:
- use database $D$ prefix-projected on some sequence $s$ (it’s called prefix-projected database)
- grow frequent subsequences from them - without generating candidates
- examine only prefix subsequences